Diviser pour régner

• Définition
• Exemples
• Complexité

Dichotomie

La dichotomie fait partie des méthodes dites "diviser pour régner". Elle consiste pour un objet de taille N à exécuter un algorithme de façon à réduire le problème à un objet de taille n/2. On répète alors l'algorithme de réduction sur ce dernier objet. Ainsi, il suffit de connaitre la résolution pour un problème de taille faible (typiquement N=1 ou N=2) pour obtenir la totalité de la résolution.
Ce type d'algorithme est souvent implémenté de manière récursive. Lorsque cette technique est utilisable, elle conduit à un algorithme très efficace et très lisible.
Il est parfois nécessaire de prétraiter les données avant d'appeler la fonction récursive. La fonction récursive est alors une fonction locale à la fonction d'appel.


Exemples

Recherche du zéro d'une fonction croissante


Soit g une fonction croissante sur un intervalle [a,b] et telle que f(a)≤0 et f(b)≥0. L'algorithme ci-dessous permet de trouver la valeur x de [a,b] telle que f(x)=0 avec une précision e.


fonction zero(ref g(val n:réel):fonction;val a,b,e:réel):réel;
  var M:réel;
    début
      M=g((a+b)/2);
      si |M|<e alors
        retourne((a+b)/2) 
      sinon 
        si M>0 alors
          zero(g,a,(a+b)/2,e)
        sinon
          zero(g,(a+b)/2,b,e)
        finsi      
      finsi      
    fin
finfonction
 

Trouver un élément dans une tableau ordonné


Nous avons déjà traité cet algorithme sous une autre forme au chapitre Tableaux.

Propriété 8.1. T un tableau d'entiers trié d'indice variant entre d et f. Posons 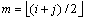. Soit e un entier appartenant à la séquence contenue dans T. On a l'une des propriétés suivantes :

• T[m]=e,
• e est dans la séquence contenu dans T[d..m-1],
• e est dans la séquence contenu dans T[m+1..f].

fonction cherche(ref T:tableau[1..N]d'entiers; val e:entier):entier;
  var d,f:entier;
  fonction chercheRec(ref T:tableau[1..N]d'entiers; val d,f,e:entier):entier;
    var m;
    début
      si f==d alors 
        si T[d]==e alors
           retourner(f)
        sinon 
           retourner(NUL)
        finsi
      sinon
        m=partieEntiere((d+f)/2);
        si T[m]<e alors
          retourner(chercheRec(T,m+1,f,e))
        sinon
          retourner(chercheRec(T,d,m,e))
        finsi
      finsi
    fin
  finfonction

  début
    d=1;
    f=N;
    retourner(chercheRec(T,d,f,e))
  fin
finfonction 

Propriété 8.2. La complexité de la fonction cherche est O(log₂(n)).

idée de la preuve La complexité de la fonction cherche est donnée par la complexité de chercheRec. Soit f(n) le nombre de test effectué par cette fonction. On a

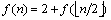
f(1)=2.
Soit p tel que 2^p≤n≤ 2^p+1. On a donc p≤log₂(n)≤ p+1. De plus

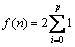
et donc f(n)=2*(p+1).


Remarque

L'algorithme de multiplication de deux matrices de dimension nxn s'implémente facilement en O(n³). Strassen a montré qu'en utilisant une méthode diviser pour régner la multiplication peut s'effectuer en O(n^ln(7)/ln(2))(courbes).

Complexité

Un algorithme diviser pour régner a la structure suivante :
1. construire une solution élémentaire pour n≤n₀
2. pour résoudre un problème de taille n>n₀, l'algorithme consiste à décomposer le problème en sous-problèmes ayant tous la taille n/b (peut-être approximativement)
3. à appliquer l'algorithme à tous les sous-problèmes
4. à construire une solution du problème en composant les solutions des sous-problèmes.
La complexité en temps de l'algorithme est donc déterminée par une équation de récurrence de la forme : C(n) = aC(n/b) + d(n)
qui après résolution permet de montrer que cette méthode conduit à des algorithmes plus efficaces en nombre d'opérations. Cependant, ceci ne doit pas occulter l'aspect mémoire. La complexité en mémoire doit rester d'un ordre raisonnable. (cf récursivité).