Complexité

---

• Définitions
• Structures de contrôle
• Exemples

Définitions

Définition 4.1.(Notation de Landau)On dit que f=O(g) s'il existe deux nombres rééls k,a > 0 tels que pour tout x>a, |f(x)|≤k|g(x)|.

Exemple 4.1.
Si le nombre d'instructions est égal à f(n)=a n² + b n + c avec a,b,c des constantes réelles, alors f(n)=O(n²).

Les figures permettent de comparer les fonctions usuelles utilisées pour décrire la complexité d'un algorithme en fonction de la taille n des données d'entrées. Parmi les fonctions usuelles, le log à base 2 de n (log₂(n)) joue un rôle important.

Pour un algorithme A, notons C_A(D), le coût de l'algorithme A pour une instance D.


Définition 4.2. On définit les trois complexités suivantes :

• Complexité dans le pire des cas
  C^>_A(n)=max{C_A(d),d donnée de taille n}
• Complexité dans le meilleur des cas C^<_A(n)=min{C_A(d),d donnée de taille n}
• Complexité en moyenne
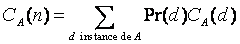
  où Pr(d) est la probabilité d'avoir en entrée une instance d parmi toutes les données de taille n.





Soit D_n l'ensemble des instances de taille n. Si toutes les instances sont équiprobables, on a
Parfois, il est nécessaire d'étudier la complexité en mémoire lorsque l'algorithme requiert de la mémoire supplémentaire (donnée auxiliaire de même taille que l'instance en entrée par exemple).



---

Structures de contrôle

Les algorithmes font intervenir les opération élémentaires suivantes:
• opérations élémentaires +,-,*,/
• test d'expression booléenne
• appel de fonctions.
Les complexités en temps des structures sont données ci-dessous
• Bloc d'instruction : somme des coûts des instructions
• Alternative
  • Alternative simple : un test
  • Alternative multiple :
    • complexité minimum : un test
    • complexité maximum : nombre de cas possible-1
• Répétition
  Soit B_T(n)(resp. B_O(n)) la complexité en nombre de tests (resp. d'opérations élémentaires) de la suite d'instructions à itérer, et k le nombre de fois ou l'itération s'effectue alors la complexité sera de .
  • k B_T(n)+1 pour le nombre de tests
  • k B_O(n) pour le nombre d'opérations du tant que et du répéter
  • k (B_O(n)+1) pour le nombre d'opérations du pour

---

Exemples

Somme des N premiers entiers

fonction suite(val n:entier):entier;
  var i,s:entier;
  début
    s=0;
    pour i allant de 1 à n faire
      s=s+i;
    finpour;
    retourner(s)
  fin
finfonction;

Source Python
On a C^>_suite(n)= C^<_suite(n)=C_suite(n)=O(n).

Apparition d'un Pile dans une suite de n lancers d'une pièce

Entrée : un entier n
Sortie : vrai si on rencontre un Pile faux sinon.
La fonction suivante retourne vrai lorsque l'un des lancers est égal à 6 et false sinon.

fonction jeuDePile(val n:integer):booléen;
  var i: entier;
  début
    pour i allant de 1 à n faire
      f=résultat_lancer_pièce()
      si (f==pile) alors
        retourner(VRAI)
      finsi
    finpour
    retourner(faux)
  fin
finFonction

Source Python
• C^>_pile(n)= O(n) (On ne tire jamais de Pile)
• C^<_pile(n)= O(1) (On tire un Pile le premier coup)
• Les faces du dé apparaissent de manière équiprobables et les tirages sont indépendants. On  peut montrer que le coût moyen de l'algorithme est C_pile(n)=O(1).