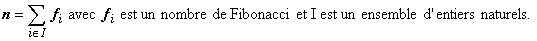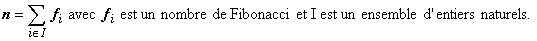Enoncé

Soit la suite dite de Fibonacci définie par :

f₀=1
f₁=1
f_n=f_n-1+f_n-2 pour n > 1

On souhaite écrire une fonction donnant le nombre de partitions d'un entier n écrites avec des nombres de la suite de fibonacci. Une telle partition est défini par :

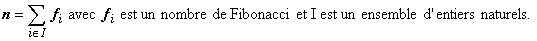Par exemple, si n=10 il y a partitions

10=8+2
10=8+1+1
10=5+3+2
10=5+3+1+1

Solution

maxFibo=1000;
fonction sacADos(val n:entier):entier;
  var fibo:tableau[0..maxFibo] d'entiers;
  var Nfibo:entier;
  var sac:tableau[1..partieEntiere(maxFibo/2)]d'entiers;
  var Nsac;entier;
  fonction fibonacci(val n:entier):vide;
    début
      fibo[0]=1;
      fibo[1]=1;
      Nfibo=1;
      tanque fibo[Nfibo]<n et Nfibo<maxFibo faire
          Nfibo=Nfibo+1;
          fibo[Nfibo]=fibo[Nfibo-1]+fibo[Nfibo-2]
      fintantque
    fin
  finfonction
  fonction sacADosRec(val p:entier;val n:entier;val tailleSac:entier):vide;
    début
      si p=0 alors
        ecrire(sac[1..tailleSac]);
        Nsac=Nsac+1;
      sinon 
        si n>=0 alors 
          si p>=fibo[n] alors
            sac[tailleSac+1]=fibo[n];
            sacADosRec(p-fibo[n],n-1,tailleSac+1);
          finsi
          sacADosRec(p,n-1,tailleSac);
        finsi
      finsi
    fin
  finfonction
  début
    fibonacci(n);
    si fibo[Nfibo]<n alors
      retourner(NULL)
    sinon
      Nsac=0;
      sacADosRec(n,Nfibo,0);
      retourner(Nsac);
    finsi
  fin
finfonction

Extension

Le problème plus général est connu sous le nome du problème du sac à dos. Il consiste à écrire toutes les partitions d'un entier à partir d'un ensemble d'entiers sans répétition. En exercice, on peut écrire cet algorithme.