1. Enoncé

    2. Décrire une structure permettant de gérer des polynômes définis sur les réels. Ecrire un ensemble de primitives associées permettant les principales opérations.

  2. Structure et primitives

    3. On note n le degré (resp. le degré maximum) du pôlynome (resp. des pôlynomes).

  3. Amélioration de la complexité

    4. Même si en première approche, la complexité ne prend en compte le nombre d'opérations (+, *), en seconde analyse, les multiplications sont beaucoup plus coûteuses que les additions. Ceci est pris en compte dans les algorithmes ci-dessous.

    L'algorithme énoncé au paragraphe précédent effectue 2n multiplications. Le schéma d'Horner d'un pôlynome permet d'effectuer n multiplication seulement. Le schéma d'Horner repose sur la propriété suivante :
    Soit P(X) un pôlynome de supérieur à 0,
    .
    Alors, P(X) s'écrit :
    .
    On en déduit le schéma de Horner
    . 
    fonction valeur(ref p:polynome;val x: réél):réél;
var s:réel;
début
  s=p.coeff[p.degre];
  pour i allant de p.degre-1 à 0 pas de -1 faire
    s=s*x+p.coeff[i]
  finpour
  retourner(s)
fin
finfonction

  4. Multiplication

    5. Une méthode diviser pour régner permet d'améliorer cet algorithme. Elle est basée sur l'égalité suivante
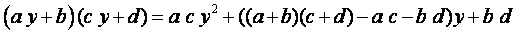    . Cette égalité signifie, entre autre, que si deux pôlynomes sont de degré 1, il suffit de trois multiplications de réels pour obtenir leur produit.
    Les quantités a, b, c, d, y étant quelconque, celles-ci peuvent être elles mêmes des polynômes. Soit le pôlynome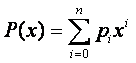
    .
    . On peut écrire P(X) sous la forme
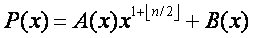    avec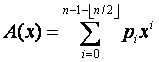
    .
    .
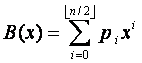    De même on a :
    ,
    ,
    ,
    .
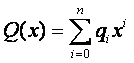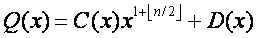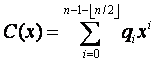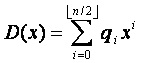    On peut donc utiliser l'équation du départ avec a=A(x), b=B(x), c=C(x), d=D(x) et
    .
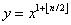    De plus, on est amené à calculer des produits de pôlynomes de degré au plus n/2. Il s'agit donc d'une méthode diviser pour régner. La complexité en nombre de multiplications est alors O(nlog23). Comme on notera ci-dessous l'algorithme est plus complexe à écrire mais il est bien plus efficace aussi.
    Un prétraitement permet de considérer des pôlynomes de même degré. Il faut donc une fonction "chapeau". On définit de plus deux autres fonctions utiles pour le calcul : 
    fonction multiplie(ref p,q:polynome):polynome;
  var p1,p2:polynome;
  fonction etend(ref p:polynome;val n:entier):polynome;
    var i:entier;
    var r:polynome;
    début
      r=decale(p,0);
      r.degre=n;
      pour i de p.degre+1 a n faire
        r.coeff[i]=0;
      finpour;
      retourner(r);
    fin
  finfonction
  fonction tronque(ref p:polynome;val n:entier)
    var c:polynome;
    var i:entier;
    début
      c.degre=n;
      pour i de 0 a n faire
        c.coeff[i]=p.coeff[i];
      finpour;
      retourner(c);
    fin
  finfonction
  fonction multirec(ref p,q:polynome)
    var a,b,c,d:polynome;
    var c0,c1,c2:réel;
    var C0,C1,C2:réel;
    var m:entier;
    début
      selon que
        cas p.degre==0 
          retourner(polynome([p.coeff[0]*q.coeff[0]]))
        cas p.degre==1 
          c0= p.coeff[0]*q.coeff[0];
          c2=p.coeff[1]*q.coeff[1];
          c1= (p.coeff[0]+p.coeff[1])*(q.coeff[0]+q.coeff[1]);
          c1=c1-c0-c2;
          retourner(polynome([c0,c1,c2]));
        autrement
          m=partieEntière(p.degre/2);
          a=decale(p,-(m+1));
          b=tronque(p,m);
          c=decale(q,-(m+1));
          d=tronque(q,m);
          C2=multirec(a,c);
          C0=multirec(b,d);
          C1=multirec(ajout(a,b),ajout(c,d));
          C1=ajout(c1,ajout(moins(c0),moins(c2)));
          C1=decale(c1,1+m);
          C2=decale(c2,2+2*m);
          C0=ajout(c0,ajout(c1,c2));
          retourner(C0);
      finselonque:
    fin
  finfonction; 
  début
    si p.degre>q.degre alors
      p1=p;
      p2=etend(q,p.degre);
    sinon
      p1=q;
      p2=etend(p,q.degre);
    finsi;
    retourner(multirec(p1,p2));
  fin
finfonction
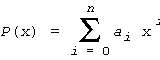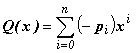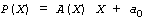
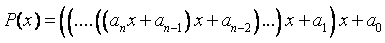
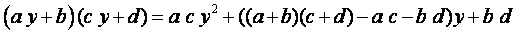
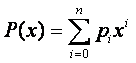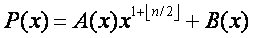
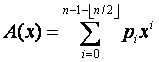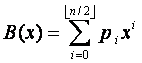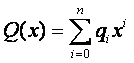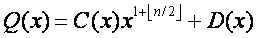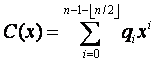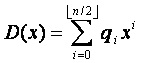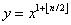