table des matières

Université Bordeaux 1

Licence Semestre 3  - Algorithmes et structures de données 1

Dernière mise à jour effectuée le 23 Juin 2014

Introduction

  1. Complexité

    2. Définition 1.1. L'efficacité d'un algorithme est mesuré par son coût (complexité)en temps et en mémoire.
    Une problème NP-complet est un problème pour lequel on ne connait pas d'algorithme correct efficace c'est à dire réalisable en temps et en mémoire. Le problème le plus célèbre est le problème du voyageur de commerce. L'ensemble des problèmes NP-complets ont les propriétés suivantes : La complexité d'un algorithme se mesure en calculant pour traiter une donnée de taille n.
    Dans ce qui suit, nous considèrerons que la complexité des instructions élémentaires les plus courantes sur un ordinateur ont un temps d'exécution que l'on considèrera dans ce cours comme constant égal à 1.
    Ce qui intéresse fondamentalement l'algorithmique c'est l'ordre de grandeur (au voisinage de l'infini) de la fonction qui exprime le nombre d'instructions ou la taille de la mémoire.
    Définition 1.2. On définit les trois complexités suivantes :
    • Complexité dans le pire des cas
      C>A(n)=max{CA(d),d donnée de taille n}
    • Complexité dans le meilleur des cas
      C<A(n)=min{CA(d),d donnée de taille n}
    • Complexité en moyenne

      où Pr(d) est la probabilité d'avoir en entrée une instance d parmi toutes les données de taille n.


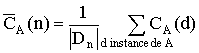
    Soit Dn l'ensemble des instances de taille n. Si toutes les instances sont équiprobables, on a

  2. Pointeur

    3. Définition 1.3. Un pointeur est une variable qui contient une adresse mémoire directe ou relative.
    On écrit pour déclarer un pointeur 
    nom_pointeur=^type_predefini;
    Par convention un pointeur qui ne donne accès à aucune adresse contient la valeur NIL.
    Pour accéder à l'emplacement mémoire désigné par le pointeur on écrit le pointeur suivi de ^. La primitive new permet d'allouer dynamiquement de la mémoire au cours d'une exécution. On écrira 
    new(nom_pointeur);
    Lorsque la mémoire n'est plus utilisée par le pointeur il faut impérativement la libérer. La primitive delete permet de libérer la mémoire allouée par l'intermédiaire d'un pointeur, on écrira 
    delete(nom_pointeur);

  3. Récursivité

    4. Définition 1.4. Lorsqu'un algorithme contient un appel à lui-même, on dit qu'il est récursif. Lorsque deux algorithmes s'appelent l'un l'autre on dit que la récursivité est croisée

    Visibilité d'une variable

    Une variable V locale est visible à l'intérieur du bloc où elle est déclarée. Une variable globale est visible de partout

    Exemple

    Soit la fonction P suivante 
    fonction f():vide
  var  i:entier;
  début
  i = 5;
  afficher(i);
  fin
finfonction

fonction appel()
  début
    i = 3;
    afficher(i);
    f();
    début
      var j:entier;
      i = 4;
      afficher(i);
    fin
  fin
finfonction

    Complexité

    Un algorithme récursif nécessite de conserver les contextes récursifs des appels. Par suite, la récursivité peut conduire à une complexité mémoire plus grande qu'un algorithme itératif.

    Exemple

    Soit les deux fonctions calculant la factorielle : 
    fonction facRecur(val n:entier):entier;
  début
    si n==0 alors 
      retourner(1)
    sinon
      retourner(n*facRec(n-1))
    finsi
  fin
finfonction

fonction facIter(val n:entier):entier;
  début
    var i,p:entier;
    p=1:
    pour i=2 à n faire
      p=p*i;
    finpour
    retourner(p)
  fin
finfonction
    La fonction factIter est meilleure en temps et mémoire (voir).
    Définition 1.5. Un algorithme récursif présente une récursivité terminale si et seulement si la valeur retournée par cet algorithme est une valeur constante ou un appel à la fonction.
    L'algorithme facRecur ne présente pas de récursivité terminale.

    Exemple

    fonction facRecurTerm(val n:entier;val res:entier):entier;
  début
    si n==0 alors 
      retourner(res)
    sinon
      retourner(facRecurTerm(n-1,n*res))
    finsi
  fin
finfonction
    L'algorithme facRecurTerm présente une récursivité terminale. La factorielle se calcule par l'appel facRecurTerm(n,1)
    L'intérêt d'une récursion terminale est que les compilateurs détectent cette propriété et optimisent le stockage de l'environnement de la fonction. Ainsi facRecurTerm aura une complexité identique à facIter.
    ATTENTION. Dans le cas d'un algorithme présentant deux appels récursifs, rendre la récursivité terminale ne permet pas obligatoirement au compilateur d'obtenir une complexité inférieure.

    Exemple

    fonction fiboIter(val n:entier):entier;
  var i,f1,f2:entier;
  début
    si n==0  alors 
      retourner(0);
    sinon
      f1=0;f2=1;
      pour i=2 à n faire
        tmp=f1+f2;
        f1=f2;
        f2=tmp;
      finpour
      retourner(f2)
    finsi
  fin
finfonction

fonction fiboRecTerm(val n:entier;val res:entier):entier;
  début
    casou
      n == 0 : retourner(res)
      n == 1 : retourner(res+1)
      autrement : retourner(fiboRecTerm(n-1, fiboRecTerm (n-2, res)));
    fincasou
  fin
finfonction
    l'appel s'effectue par fiboRecTerm(n,0).
    Dans ce qui précède, lors de l'appel de la fonction, le paramètre est précédé du mot val. Ce mot clé indique que le paramètre est passé par valeur. La valeur fournie à l'appel sera recopié dans le paramètre dans l'environnement de la fonction.
    On peut faire précéder le paramètre du mot clé ref. Ce mot clé indique que le paramètre est passé par référence. C'est l'adresse du (ou encore le pointeur vers le) paramètre fourni à l'appel qui sera copiée dans l'environnement de la fonction.
    Voir un exemple ici.

  4. Type abstrait

    5. Définition 1.6. Un type abstrait est un triplet composé :
    • d'un nom,
    • d'un ensemble de valeurs,
    • d'un ensemble d'opérations (souvent appelé primitives) définies sur ces valeurs.
    D'un point de vue complexité, on considère que les primitives (à part celle d'initialisation si elle existe) ont une complexité de temps et de mémoire en O(1). Pour désigner un type abstrait on utilise une chaine de caractères.
    Exemple
    Les nombres complexes ne sont pas des types de bases. On peut les définir comme un type abstrait :
    • nom : nombreComplexe
    • ensemble de valeur : réel X réél
    • primitives :
      • multiplication : (nombreComplexe X nombreComplexe) → nombreComplexe
      • addition : (nombreComplexe X nombreComplexe) → nombreComplexe
      • module : nombreComplexe → réel

  5. Containeur

    6. Définition 1.7. Une containeur est un type abstrait permettant de représenter des collections d'objets ainsi que les opérations sur ces objets.
    Les collections que l'on veut représenter peuvent être ordonnés ou non ordonnés, numériques ou non. L'ordre est parfois fournit par un évènement extérieur. Les collections d'objets peuvent parfois contenir des éléments identiques.

    Accès

    valeur : containeur → objet

    Modification

    creerContaineur: containeur → vide
    ajouter : containeur X objet → vide
    supprimer : containeur X objet → vide
    detruireContaineur : containeur → vide
    Exemple
    Un ensemble de nombres complexes peut être défini par un containeur dont les objets sont des nombreComplexe.

  6. Implémentation

    7. Définition 1.8. L'implémentation consiste à choisir une structure de donnée et les algorithmes associés pour réaliser un type abstrait.
    La structure de donnée utilisée pour l'implémentation peut elle-même être un type abstrait. L'implémentation doit respecter la complexité des primitives à part celle d'initialisation (celle-ci ne s'exécutera qu'une fois).
    Exemple
    Le type abstrait nombreComplexe peut être implémenté de la manière suivante : 
    type nombreComplexe=structure
                           r:réél;
		           i:réel;
	                 finstructure
fonction op::*(val a,b:nombreComplexe):nombreComplexe;
  var c:nombreComplexe;
  début
    c.r=a.r*b.r-a.i*b.i;
    c.i=a.r*b.i+a.i*b.r;
    retourner(c)
  fin
fonction op::+(val a,b:nombreComplexe):nombreComplexe;
  var c:nombreComplexe;
  début
    c.r=a.r+b.r;
    c.i=a.i+b.i;
    retourner(c)
  fin
fonction module(val a:nombreComplexe):réel;
  début
    retourner(sqrt(a.r*a.r+a.i*a.i))
  fin
    Exemple
    Un containeur de nombreComplexe peut être implémenté par un tableau de nombreComplexe. 
    containeur d'objet=tableau[1..N]de 
             structure
               v:objet;
	       b:booleen;
             finstructure

    Modification

    fonction creerContaineur(ref T:containeur de nombreComplexe):vide;
  var i:entier;
  début
    pour i allant de 1 à N faire
      T[i].b=faux;
    finPour;
  fin
fonction ajouter(ref C: containeur de nombreComplexe;val x:nombreComplexe):vide
  var i:entier;
  début
    i=1;
    tant que i<n et C[i].b faire
      i=i+1;
    fintantque
    si i<=n alors
      C[i].v=x;
      C[i].b=vrai
    finsi
  fin
fonction supprimer(ref C: containeur de nombreComplexe;val x:nombreComplexe):vide
  var i:entier;
  début
    i=1;
    tant que i<=n et C[i].v!=x faire
      i=i+1;
    fintantque
    si i<=n alors
      C[i].b=faux
    finsi
  fin
fonction detruireContaineur(ref C : containeur de nombreComplexe):vide
  début
    pour i allant de 1 à N faire
      C[i].b=faux;
    finPour;
  fin

    Accès

    fonction valeur(ref C : containeur de nombreComplexe):nombreComplexe;
/* retourne le premier nombre complexe /*
  var i:entier;
  début
    i=1;
    tant que i<n et !C[i].b faire
      i=i+1;
    fintantque
    si i<=n alors
      retourner(C[i].v)
    sinon
      retourner(NULL)
    finsi
  fin

  7. Quelques remarques importantes

    8. Soit B une expression booléenne, ne jamais écrire 
    si B alors retourner(vrai) sinon retourner(faux) finsi
    On écrit toujours 
    retourner(B)

    Ne pas confondre la valeur NIL qui est une valeur de pointeur et signifie que le pointeur est non affecté avec la valeur NULL qui correspond à une valeur de la variable sans signification.
    Exemple
    Le type abstrait nombreComplexe peut être implémenté en utilisant la valeur NULL de la manière suivante: 
    containeur de NombreComplexe=tableau[1..N]de nombreComplexe;

    Modification

    fonction creerContaineur(ref T:containeur de nombreComplexe):vide;
  var i:entier;
  début
    pour i allant de 1 à N faire
      T[i]=NULL;
    finPour;
  fin
    Un excellent exercice consiste à réécrire les toutes les fonctions du container puis à l'implémenter en C.