Table de Hashage
- Définitions
- Fonction de hachage
- Adressage chainé
- Adressage ouvert
- Réorganisation d'une table de hachage
Rappel
Soit a et b deux entiers et q et r respectivement leur quotient et reste dans la divistion Euclidienne, on a- Définitions
Définition 9.1. Soit K un ensemble de valeurs et m un entier naturel, une fonction de hachage hm est une fonction définie de K dans {0,...,m-1}.
Les éléments de K sont appelées clés. Si k est une clé, h(k) est dite valeur de hachage de k.Définition 9.2. Soit m un entier naturel et hm une fonction de hachage, une table de hachage est un containeur tel que
Remarques- le nombre d'éléments de la table (dimension ou taille) est fixe,
- l'accès aux éléments s'effectue indirectement par la valeur de hachage de la clé.
- Les tables de hachage sont très utiles dans le cas où l'amplitude des clés est grande (structure de tableau non utilisable) et les éléments à gérer sont "assez figés" ce qui permet d'espérer un temps d'accès à l'information proche de O(1) (structure de liste trop pénalisante).
- Pour une séquence d'élément, il est clair qu'il peut exister deux clés k1 et k2 de K telles que hm(k1)=hm(k2), on dit alors qu'il y a collision des clés k1 et k2.
- Soit p dans [0..m-1], il est possible qu'il n'existe pas de clé k dans K telle que hm(k)=p.
La sructure de données pour représenter une table de hachage est un tableau de dimension [0..m-1]. Pour une clé k de K, T[hm(k)] donne l'accès à l'élément de clé k. On précisera ces moyens d'accès aux paragraphes concernant la gestion des collisions : adressage chainé , adressage ouvert.
On nommera le type abstrait tableHash. La valeur de hashage d'une clé est donc un curseur. Les primitives d'accès à une table de hashage sont :- accès
fonction chercher(ref T:tableHash de clés, val v:clé):curseur; - modification
fonction créerTableHachage(ref T: tableHash de clé, ref h:fonction):vide; fonction ajouter(ref T:tableHash de clé,val x:clé):booleen; fonction supprimer((ref T:tableHash de clé,val x:clé):vide;
- Fonctions de hachage
Les fonctions de hachage doivent pouvoir s'appliquer sur tout type de base. Les types numériques peuvent aisément être ramené à un entier.
Pour les chaines de caractères, il est toujours possible de leur associer de manière bijective un entier. Considérons la fonction asc qui a un caractère associe son code ASCII (code sur 7 bits). Soit c0...cp une suite de p caractères alors la valeur entière associée bijectivement est
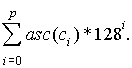
Méthode de division
Soit m un entier premier pas trop proche d'une puissance de 2,
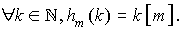
Méthode de multiplication
Soit m=2p et A dans ]0..1[,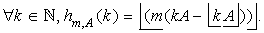
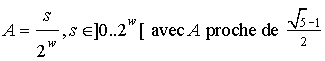
Famille de hashage universel
Definition 9.3. Soit H un ensemble de fonction de hachage de U dans [0..m[. On dit que la famille H est universelle si pour toutes clés k1, k2 dans U, le nombre de fonctions h de H telles que h(k1)=h(k2) est égal à card(H)/m.
Soit m un entier naturel. Soit p un nombre premier grand tel que
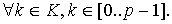


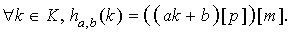
Theorem 9.4. La famille de fonction
De ce fait, On peut montrer que l'exécution de n primitives a une complexité moyenne en O(n).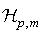 est universelle.
est universelle.
- Adressage chainé
Definition 9.5. L'adressage d'une table de hashage est dit chainé si l'élements i du tableau donne accès à une structure de données permettant de stocker les clés k telles que hm(k)=i.
Les valeurs sont donc stockées à l'extérieur de la table qui est un tableau de pointeurs. Par suite, si il n'existe pas de clé k telle que hm (k)=i alors T[i]=NIL.
L'espace de stockage des clés peut être une liste doublement chainée. On a dans ce castableHash de clé=structure table:tableau[0..m-1] de listeDC de clé; h:fonction(val v:clé):entier finstructure- accès
fonction chercher(ref T:tableHash de clé, val e:entier):curseur; début retourner(chercher(T.table[T.h(e)],e)) fin - modification
fonction créerTableHach(ref T: tableHash de clé, ref h:fonction):vide; var i:entier; début pour i allant de 0 à m-1 faire creerListe(T.table[i]) finpour T.h=h; fin fonction ajouter(ref T:tableHash de clé,val e:entier):booleen; début insererEnTete(T.table[T.h(e)],e); retourner(vrai): fin fonction supprimer(ref T:tableHash de clé,val e:entier):vide; début supprimer(T.table[T.h(e)],e)) fin
Théorème 9.6. Dans une table de hashage à adressage chainé, une recherche fructueuse ou infructueuse prend en moyenne O(1+n/m) si chaque élément à les mêmes chances d'être haché vers l'une quelconque des cases indépendamment des autres éléments (hachage uniforme).
- Adressage ouvert
Definition 9.7. L'adressage d'une table de hashage est dit ouvert si les élements du tableau sont les clés elles mêmes.
Les éléments de la table sont donc initialisés à NULL. La gestion de la collision se fait en trouvant une place libre dans la table. Pour cela on utilise une seconde fonction s(x,i) à valeur dans [0..m] que l'on compose avec hm(k). Cette seconde fonction dite de sondage doit vérifier les propriétés suivantes :- s(hm(k),0)=hm(k)
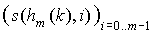 est une permutation de la séquence (i)i=0..m-1.
est une permutation de la séquence (i)i=0..m-1.
Quelques méthodes de sondage
- Sondage linéaire : s(k,i)=(h(k)+i)[m]
- Sondage quadratique : s(k,i)=(h(k)+c1 i+c2 i2)[m]
- Double hachage : s(k,i)=(h(k)+i h'(k))[m] où h' est une seconde fonction de hashcode telle que

tableHash de clé=structure table:tableau[0..m-1] de clé; h:fonction(val v:clé):entier s:fonction(val v:clé):entier finstructure- accès
fonction chercher(ref T:tableHash de clé, val e:entier):curseur; var i:entier; début i=0; tant que T.table[T.s(T.h(e),i)]!=e et i<m faire i=i+1 fintantque si i==m alors retourner(NULL) sinon retourner(T.s(T.h(e),i)) finsi fin - modification
fonction créerTableHachage(ref T: tableHash de clé, ref h:fonction(var x:entier):entier) ref s:fonction(var x:entier):entier):vide; var i:entier; début pour i allant de 0 à m-1 faire T.table[i]=NULL; finpour T.h=h; T.s=s; fin fonction ajouter(ref T:tableHash de clé,val e:entier):booleen; var i:entier; début i=0; tant que T.table[T.s(T.h(e),i)]!=NULL et i<m faire i=i+1 fintantque si i==m alors retourner(faux) sinon T.table[T.s(T.h(e),i)]=e; retourner(vrai) finsi fin fonction supprimer(ref T:tableHash de clé,val e:entier):vide; var p:curseur; début p=chercher(T,e); si p!=NULL T[p]=NULL finsi fin
Théorème 9.8. Etant donné une table de hachage de facteur de remplissage r, une recherche infructueuse ou l'insertion d'une clé se fait en moyenne en 1/(1-r), si chaque élément à les mêmes chances d'être haché vers l'une quelconque des cases indépendamment des autres éléments (hachage uniforme ).
Théorème 9.10. Etant donné une table de hachage de facteur de remplissage r, une recherche fructueuse se fait en moyenne en (1/r)*ln(1/(1-r)), si chaque élément à les mêmes chances d'être haché vers l'une quelconque des cases indépendamment des autres éléments (hachage uniforme ).
- Réorganisation d'une table de hachage Le taux d'occupation de la table doit rester relativement faible pour minimiser le risque de collision sinon le nombre de collision augmente et la performance se dégrade. Ceci veut dire qu'on ajoute à chaque type abstrait un champ "taux de remplissage".
Redimentionner à l'intérieur de la table
On realloue un espage plus grand (on multiplie souvent par 2) et on marque l'ensemble des clés à vrai. Pour chaque clé k marquée vrai, on calcule h(k):- si h(k) est libre on place k et on la marque à faux,
- si h(k) est occupée par une clé k', on place k on la marque à faux et on réitère le procédé avec k'
Redimentionner à l'extérieur de la table
On alloue un nouveau tableau. Pour initialiser le tableau :- soit on reaffecte les clés dans la nouvelle structure de donnée, puis on détruit l'ancienne table.
- soit on affecte toute nouvelle clé dans la nouvelle structure de donnée et lors de cette affectation on enlève p éléments de l'ancienne structure de donnée pour les mettre dans la nouvelle. L'ancienne structure est détruite lorsque elle est vide.
- accès