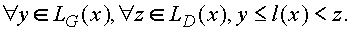- Arbre binaire de recherche
Définition 8.1.Soit x un sommet interne d'étiquette l(x), LG(x) (resp. LD(x)), l'ensemble des étiquettes du sous arbre gauche (resp. droit) de x. On a
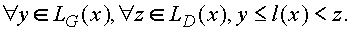
Propriété 8.2 Si on parcourt un arbre binaire de recherche en ordre infixe, on obtient une séquence d'étiquettes triées en ordre croissant.
Corollaire 8.3 Si n est le nombre de sommets d'un arbre binaire de recherche, on obtient la liste triée en O(n).
On utilise les primitives des arbres binaires.
Recherche d'un élément dans un sous arbre
fonction recherche(x:sommet, val e:objet):sommet;
var tmp:objet;
début
si x==NIL alors
retourner(NIL)
sinon
tmp= getValeur(x);
si tmp==e alors
/* on retourne le premièr sommet correspondant à la valeur */
retourner(x);
sinon
si e <tmp alors
retourner(recherche(filsGauche(x),e));
sinon
retourner(recherche(filsDroit(x),e));
finsi
finsi
finsi
fin
Complexité
- minimum : O(1)
- maximum : O(h(x))
Recherche du plus petit élément d'un sous arbre
fonction cherchePlusPetit(val x: sommet):sommet;
début
tantque filsGauche(x)!=NIL faire
x=filsGauche(x);
fintantque
retourner(x);
fin
Complexité
- minimum : O(1)
- maximum : O(h(x))
Recherche du plus grand élément d'un sous arbre
fonction cherchePlusGrand(val x: sommet):sommet;
début
tantque filsDroit(x)!=NIL faire
x=filsDroit(x);
fintantque
retourner(x);
fin
Complexité
- minimum : O(1)
- maximum : O(h(x))
Recherche de l'élément suivant une valeur présente dans un sous-arbre
fonction chercheSuivant(val x: sommet,val e:objet):sommet;
var p:sommet;
début
x=cherche(x,e);
si x==NIL alors
retourner(NIL);
sinon
si filsDroit(x)!=NIL alors
retourner(cherchePlusPetit(filsDroit(x))
sinon
p=pere(x);
tantque p!=NIL faire
si filsGauche(p)==x alors
retourner(p)
sinon
x=p;
p=pere(p);
finsi
fintantque
retourner(NIL);
finsi
finsi
fin
Complexité
- minimum : O(1)
- maximum : O(h(x))
- Modification d'un arbre binaire de recherche
Un ABR est un containeur. On peut toujours imaginer que la fonction
valeur renvoit par exemple la valeur la plus petite. Les primitives
ajouter et supprimer des objets permettent de faire évoluer un ABR.
fonction ajouter(ref x:sommet, val e:objet):vide;
var s:sommet;
début
si e ≤ valeurSommet(x) alors
s=filsGauche(x);
si s==NIL alors
ajouterFilsGauche(x,e);
sinon
ajouter(s,e);
finsi
sinon
s=filsDroit(x);
si s==NIL alors
ajouterFilsDroit(x,e);
sinon
ajouter(s,e);
finsi
finsi
fin
Complexité
- minimum : O(1)
- maximum : O(h(x))
fonction supprimer(ref x:sommet):vide;
var p,f,y:sommet;
début
si estFeuille(x) alors
p=pere(x);
si filsGauche(p)==x alors
supprimerFilsGauche(p)
sinon
supprimerFilsDroit(p)
finsi
sinon
f=filsDroit(x);
si f!=NIL
y=cherchePlusPetit(f);
tant que valeur(père(y))=valeur(y) faire
y=pere(y)
fintantque
sinon
f=filsGauche(x);
y=cherchePlusGrand(f);
finsi
v=getValeur(y);
supprimer(y);
setValeur(x,v);
finsi
fin
Complexité
- minimum : O(1)
- maximum : O(h(x))
- Equilibrage
La complexité des opérations sur un ABR dépendant de la hauteur de l'arbre, il est important qu'un ABR reste aussi proche que possible d'un arbre binaire parfait de manière à ce que la hauteur soit minimum.
L'équilibrage d'un ABR peut-être obtenu par un algorithme de type "diviser pour régner".
On récupère la liste des éléments triés dans un tableau T[1..N] où N est la taille de l'arbre de départ et on reconstruit l'arbre.
fonction lister(val x:sommet,
ref T:tableau[1..N] d'objet):vide;
ref iT:entier):vide
début
si estFeuille(x)alors
iT=iT+1;T[iT]= getValeur(x);
sinon
si filsGauche(x)!=NIL alors
lister(filsGauche(x),T,iT);
finsi
iT=iT+1;T[iT]= getValeur(x);
si filsDroit(x)!=NIL alors
lister(filsDroit(x),T,iT);
finsi
finsi
fin
L'appel
liste(A,T,0)
fournit, en utilisant l'ordre infixe, dans le tableau T la liste des valeurs dans l'ordre croissant de l'arbre A.
fonction detruireArbreBinaire(ref A:arbreBinaire d'objet):vide;
début
si s!=NIL alors
detruireArbreBinaire(filsGauche(s));
supprimerFilsGauche(s);
detruireArbreBinaire(filsDroit(s));
supprimerFilsDroit(s);
finsi
fin
fonction equilibre(ref A:arbreBinaire de objet):vide;
var N:entier;
début
N=tailleArbre(A);
var T:tableau[1..N]d'objet;
lister(A,T,0);
detruireArbreBinaire(A);
delete(A);
A=construire(T,1,N))
fin
fonction construire(ref T:tableau[1..N]d'objet,
ref d,f:entier):sommet;
var m:entier;
var c,s:sommet;
début
si d≤f alors
m=partieEntiere((d+f)/2);
new(c);
setValeur(c,T[m]);
si d==f alors
c^.gauche=NIL;
c^.droit=NIL;
retourner(c);
sinon
s=construire(d,m-1);
c^.gauche=s;
si s!=NIL alors
s^.pere=c;
finsi
s=construire(m+1,f);
c^.droit=s
si s!=NIL
s^.pere=c;
finsi
finsi
retourner(c);
sinon
retourner(NIL)
finsi
fin