Université Bordeaux 1

Arbre AVL

---

• Arbre AVL
• Facteur d'équilibrage et rotation
• Implémentation

Arbre AVL

Définition 10.1.Un arbre AVL est un arbre binaire éventuellement vide tel que

• la différence de hauteur entre le sous arbre gauche et le sous arbre droit d'un noeud différe d'au plus 1.
• les arbres gauches et droits d'un sommet sont des arbres AVL.



Le nom AVL vient du nom des auteurs G.M. Adelson-Velsky et E.M.Landis (1982).

Propriété 10.2. Si n est le nombre de noeuds d'un arbre AVL alors sa hauteur est log₂(n)

---

Facteur d'équilibrage et rotation

Chaque noeud contient un entier appelé facteur d'équilibrage qui permet de déterminer si il est nécessaire de rééquilibrer l'arbre.

Définition 10.3. Soit s un sommet ayant pour sous arbre gauche (resp.droit) G_s(rep. D_s). Le facteur d'équilibrage eq(s) du sommet s est défini par eq(s)= h(D_s)-h(G_s) avec h(NIL)=0 et si A est un arbre h(A)=hauteur(A)+1.

Le facteur d'équilibrage d'un noeud d'un arbre AVL vaut 0,1 ou -1. Lors d'insertion ou suppression, l'arbre peut se déséquilibrer (valeur 2 ou -2), on utilise alors des rotations pour rééquilibrer l'arbre.

Définition 10.4. Une rotation droite autour du sommet y d'un arbre binaire de recherche consiste à faire descendre le sommet y et à faire remonter son fils gauche x sans invalider l'ordre des éléments. L'opération inverse s'appelle rotation gauche autour du sommet x.

Dans la rotation seuls les facteur d'équilibrage de X et Y sont modifiés. Notons eq'(X) et eq'(Y) les facteurs d'équilibrage après rotation.

Propriété 10.5. Après une rotation droite autour du sommet Y, on a :

• eq'(X)=eq(X)+1+max(eq'(Y),0)
• eq'(Y)=eq(Y)+1-min(eq(X),0)

Propriété 10.6. Après une rotation gauche autour du sommet X. , on a :

• eq'(X)=eq(X)-1-max(eq(Y),0)
• eq'(Y)=eq(Y)-1+min(eq'(X),0)

---

Opérations d'insertion et suppression

Les opérations d'insertion et suppression sont celles d'un arbre binaire de recherche dans lesquelles on ajoute la gestion du facteur d'équilibrage.

• Insertion

  L'insertion aboutit à la création d'une feuille f. Considérons le premier ancêtre y de cette feuille qui viole la condition AVL, on a eq(y)=-2 ou eq(y)=2 et ces deux cas sont symétriques. Supposons que eq(y)=-2 et soit x le fils gauche de y. On a deux cas.
  • soit eq(x)=-1 , on effectue une rotation droite,
  • soit eq(x)=1, alors x a un sous arbre droit de racine z, qui a deux sous arbres. On effectue une rotation gauche autour de x puis une rotation droite autour de y.
  La hauteur du nouveau sous arbre a même hauteur que le sous arbre de départ. Il suffit donc d'une opération d'équilibrage pour que l'arbre soit AVL. Le cas eq(y)=2 est obtenue par symétrie.

• Suppression

  La suppression aboutit à la suppression d'une feuille . Considérons le premier ancêtre y de cette feuille qui viole la condition AVL, on a eq(y)=-2 ou eq(y)=2 et ces deux cas sont symétriques. Supposons que eq(y)=-2 et soit x le fils gauche de y et t le fils droit de y. La feuille a été supprimée dans le sous arbre de racine t. On a trois cas.
  • soit eq(x)=-1 , on effectue une rotation droite,
  • soit eq(x)=0 , on effectue une rotation droite,
  • soit eq(x)=1, alors x a un sous arbre droit de racine z, qui a deux sous arbres. On effectue une rotation gauche autour de x puis une rotation droite autour de y.
  La hauteur du nouveau sous arbre a même hauteur que le sous arbre de départ si le facteur d'équilibrage de la racine est 0. Dans ce cas, il suffit donc d'une opération d'équilibrage pour que l'arbre soit AVL. Dans les autres cas il faut recommencer la même opération en remontant dans l'arbre. Le cas eq(y)=2 est obtenue par symétrie.
Figures complètes ici

---

Implémentation

L'intérêt du facteur d'équilibrage est que cette information nécessite 2 bits. Néammmoins les algorithmes permettant la gestion de eq sont délicats. Dans la suite, une cellule pour un arbre AVL doit contenir un champ supplémentaire qui est la hauteur.

type celluleAVL=structure 
         info:objet;
         hauteur:entier;
         gauche:sommet;
         droit:sommet;
         père:sommet;
       finstructure
sommetAVL=^celluleAVL;

On accède à ce nouveau champ par les deux primitives suivantes :

fonction getHauteur(ref S:sommet):entier;
/* 1 pour une feuille; 0 si NIL/*
fonction setHauteur(ref S:sommet; val h:sommet):entier;
/* 1 pour une feuille; 0 si NIL/*

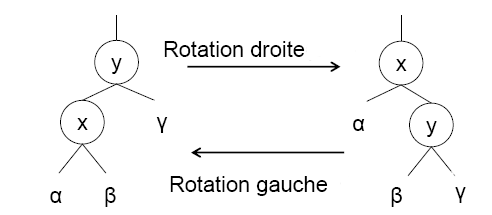
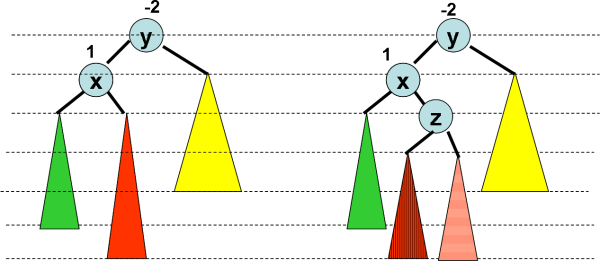
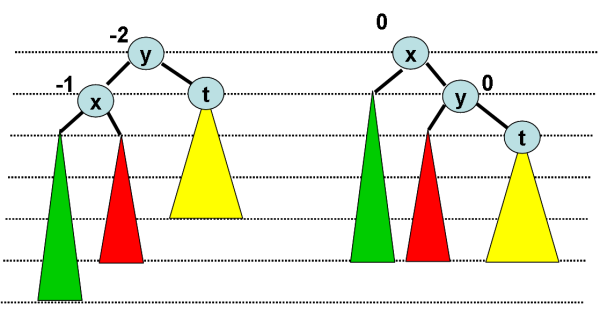
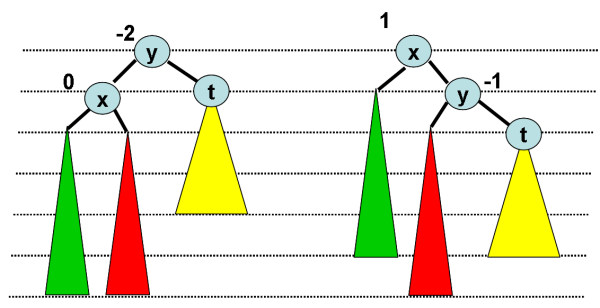
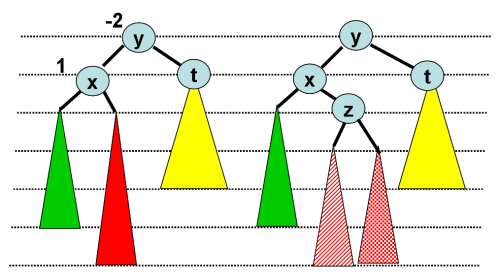
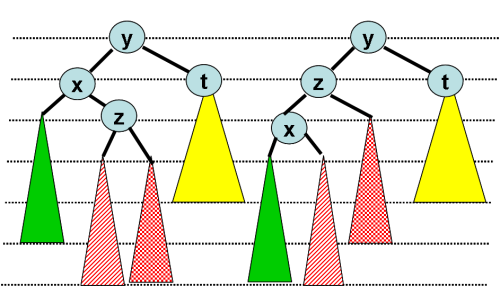
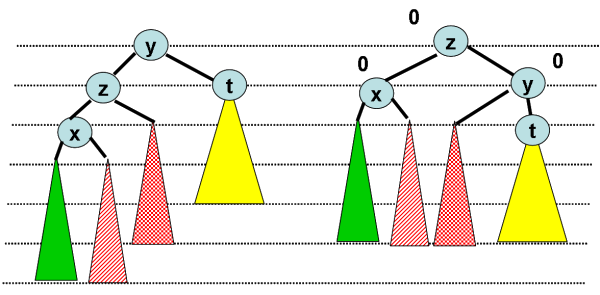
Les fonctions implémentant les rotations sont immédiates.

fonction rotationDroite(ref y:sommet):vide;
  var x,p:sommet;
  début
    x=filsGauche(y);
    p=pere(y);
    si p!=NIL alors
      si y=filsGauche(p) alors
        p^.gauche=x;
      sinon
        p^.droit=x;
      finsi
    finsi
    x^.pere=p;
    y^.pere=x;
    y^.gauche=x^.droit;
    x^.droit=y;
    setHauteur(y,max(getHauteur(filGauche(y)),getHauteur(filsDroit(y)))+1);
    setHauteur(x,max(getHauteur(filGauche(x)),getHauteur(filsDroit(x)))+1);
  fin

fonction rotationGauche(ref x:sommet):vide;
  var y,p:sommet;
  début
    y=filsDroit(x);
    p=pere(x);
    si p!=NIL alors
      si x=filsGauche(p) alors
        p^.gauche=y;
      sinon
        p^.droit=y;
      finsi
    finsi
    y^.pere=p;
    x^.pere=y;
    x^.droit=y^.gauche;
    y^.gauche=x;
    setHauteur(x,max(getHauteur(filGauche(x)),getHauteur(filsDroit(x)))+1);
    setHauteur(y,max(getHauteur(filGauche(y)),getHauteur(filsDroit(y)))+1);
  fin

Les fonctions d'insertion et suppression doivent prendre en compte le calcul du facteur d'équilibrage ainsi que le maintien de cet équilibre.

fonction ajouter(ref x:sommet, val e:objet):vide;
  var s:sommet;
  début
    si e ≤ getValeur(x) alors
      s=filsGauche(x);
      si s==NIL alors
        ajouterFilsGauche(x,e);
        setHauteur(filsGauche(x),1)
        equilibreAprèsInsertion(filsGauche(x))
      sinon
        ajouter(s,e);
      finsi
    sinon
      s=filsDroit(x);
      si s==NIL alors
        ajouterFilsDroit(x,e);
        setHauteur(filsDroit(x),1);
        equilibreAprèsInsertion(filsDroit(x))
      sinon
        ajouter(s,e);
      finsi
    finsi
  fin

fonction supprimer(ref x:sommet):booléen;
  var p,f,y:sommet;
  début
    si estFeuille(x) alors 
      p=pere(x);
      si filsGauche(p)==x alors
        supprimerFilsGauche(p)
        setHauteur(p,getHauteur(filsDroit(p)+1))
      sinon
        supprimerFilsDroit(p)
        setHauteur(p,getHauteur(filsGauche(p)+1))
      finsi
      equilibreAprèsSuppression(p)
    sinon
      f=filsDroit(x);
      si f!=NIL
          y=cherchePlusPetit(f);
      sinon
          f=filsGauche(x);
          y=cherchePlusGrand(f);
      finsi
      setValeur(x,getValeur(y));
      supprimer(y);
    finsi
  fin

fonction equilibreAprèsInsertion(ref x:sommet,val cote:entier):vide;
  var eq:entier;
  var s,p:sommet;
  début
    eq=0;
    p=x;
    tantque pere(p)!=NIL et eq!=2 et eq!=2 faire
      s=p;
      p=pere(s);
      setHauteur(p,max(getHauteur(filGauche(p)),getHauteur(filsDroit(p)))+1);
      eq=getHauteur(filsDroit(p))-getHauteur(filsGauche(p));
    fintantque   
    si eq==2 ou eq==-2 alors
      equilibreUnSommet(p,s);
    finsi
  fin

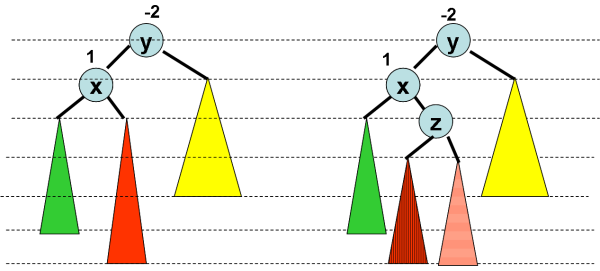
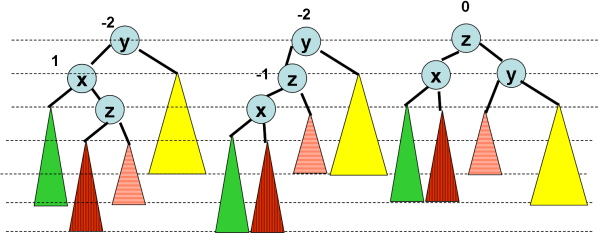
Dans le cas de suppression, on remonte à partir de la feuille supprimée dans l'arbre et de la même manière on détecte les noeuds déséquilibrés. Il est possible que plusieurs rotations soient nécessaires. En effet un déséquilibre peut en entrainer un autre.

fonction equilibreAprèsSuppression(ref x:sommet):vide;
  var eq:entier;
  var s,p:sommet;
  début
    eq=1;
    p=x;
    p=pere(s);
    tantque p!=NIL et eq!=0 faire
      s=p;
      p=pere(p);
      setHauteur(p,max(getHauteur(filGauche(p)),getHauteur(filsDroit(p)))+1);
      eq=getHauteur(filsDroit(p))-getHauteur(filsGauche(p));
      equilibreUnSommet(p,s);
    fintantque
  fin

fonction equilibreUnSommet(ref p,s:sommet):vide;
  début
    si s==filsGauche(p) alors
      si getEquilibre(p)==-2 alors 
        si getEquilibre(s)<1 alors
          rotationDroite(p);
        sinon 
          rotationGauche(s);
          rotationDroite(p);
        finsi
      finsi
    sinon
      si getEquilibre(p)==2 alors 
        si getEquilibre(s)>-1 alors
	    rotationGauche(p)
        sinon 
          rotationDroite(s);
          rotationGauche(p);
	finsi          
      finsi
    finsi
fin