Suppression

La suppression est beaucoup plus difficile que l'insertion. Le problème est la suppression d'un nud interne. En principe, il n'est pas possible en général de supprimer un nud interne, car un tel nud peut avoir deux fils et le remplacer par l'un des deux provoque la perte de l'autre.

La méthode que nous allons utiliser est de considérer trois cas :

• si le nud n'a pas de fils gauche, le remplacer par le sous-arbre droit,
• si le nud n'a pas de fils droit, le remplacer par le sous-arbre gauche,
• sinon, supprimer la cellule contenant le plus grand objet dans le sous-arbre gauche et remplacer le contenu de la cellule par cet objet.

Les figures 23.10, 23.11 et 23.12 montrent la suppression de l'élément 28 de l'arbre dans la figure 23.9.

Figure 23.10: Suppression dans un arbre binaire de recherche

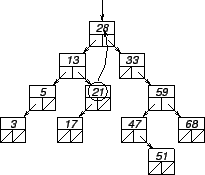Figure 23.11: Suppression dans un arbre binaire de recherche

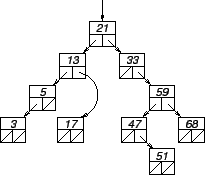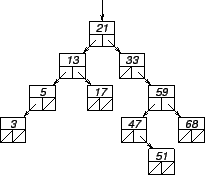
Figure 23.12: Suppression dans un arbre binaire de recherche

Voici le code correspondant :

(defun btree-delete (elem tree &key (test #'<) (key #'identity))
  (cond ((null tree) (values nil nil))
        ((funcall test
                  elem
                  (funcall key (bincell-elem tree)))
         (multiple-value-bind (ltree deleted)
             (btree-delete elem (bincell-left tree)
                           :test test :key key)
           (setf (bincell-left tree) ltree)
           (values tree deleted)))
        ((funcall test
                  (funcall key (bincell-elem tree))
                  elem)
         (multiple-value-bind (rtree deleted)
             (btree-delete elem (bincell-right tree)
                           :test test :key key)
           (setf (bincell-right tree) rtree)
           (values tree deleted)))
        ((null (bincell-left tree))
         (values (bincell-right tree) t))
        ((null (bincell-right tree))
         (values (bincell-left tree) t))
        (t (labels ((delete-largest (tree)
                      (if (null (bincell-right tree))
                          (values (bincell-left tree)
                                  (bincell-elem tree))
                          (multiple-value-bind (rtree elem)
                              (delete-largest (bincell-right tree))
                            (setf (bincell-right tree) rtree)
                            (values tree elem)))))
             (multiple-value-bind (ltree elem)
                 (delete-largest (bincell-left tree))
               (setf (bincell-left tree) ltree
                     (bincell-elem tree) elem)
               (values tree t))))))

On remarque l'utilisation d'une fonction locale récursive, définie avec labels.