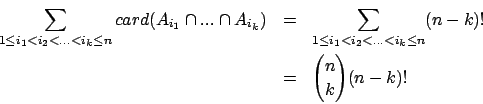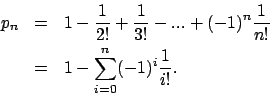suivant: À propos de ce
Principe d'inclusion-exclusion
Proposition. Soit 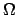 un ensemble. Soient
un ensemble. Soient
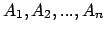 une famille de
une famille de 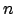 sous-ensembles de
sous-ensembles de 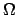 . On
a :
. On
a :
et si
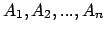 sont tous de cardinal fini, alors :
sont tous de cardinal fini, alors :
Preuve. Nous avons clairement :
Donc, la première relation est vraie pour 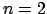 . Supposons la vraie pour
. Supposons la vraie pour 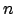 et prouvons-la pour
et prouvons-la pour  .
On a :
.
On a :
Pour démontrer la deuxième relation dans le cas des parties
finies, il suffit d'appliquer l'égalité
 au membre de la première relation.
au membre de la première relation.
Une application : Problème des chapeaux
Problème. En entrant, chacun des 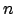 convives confie son chapeau au
vestiaire et il le reprend en partant. Au moment de départ une
panne d'électricité survient et chacun prend un chapeau au
hasard. Quelle est la probabilité pour que, au moins, un des convives ait son
propre chapeau ? Quelle en est la limite lorsque
convives confie son chapeau au
vestiaire et il le reprend en partant. Au moment de départ une
panne d'électricité survient et chacun prend un chapeau au
hasard. Quelle est la probabilité pour que, au moins, un des convives ait son
propre chapeau ? Quelle en est la limite lorsque
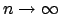 ?
?
Solution. On part du principe que la probabilité d'un événement
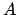 est le rapport entre le nombre de cas favorables à
est le rapport entre le nombre de cas favorables à 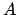 et le
nombre total de cas possibles.
et le
nombre total de cas possibles.
Le nombre total de répartitions possibles est 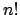 . Si
. Si 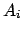 désigne
l'événement ``le
désigne
l'événement ``le 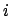 -ème invité a eu son propre
chapeau'', la probabilité
-ème invité a eu son propre
chapeau'', la probabilité  recherchée vaut :
recherchée vaut :
Nous avons, par ailleurs :

En appliquant le principe d'inclusion-exclusion à
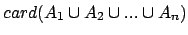 , il vient :
, il vient :
Si
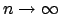 ,
,  tend vers
tend vers 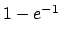 , ce qui vaut approximativement
, ce qui vaut approximativement 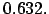



suivant: À propos de ce
Maylis Delest
2004-10-05
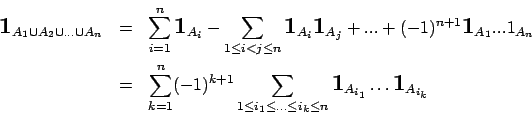
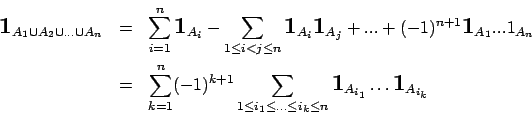
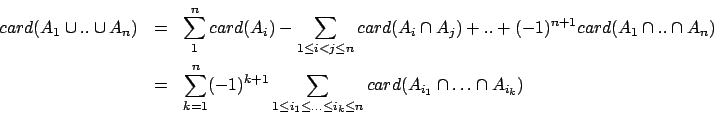
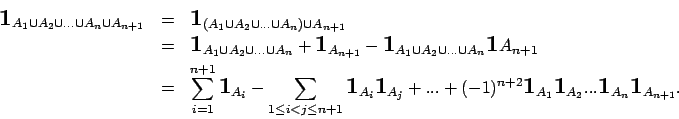
![]() au membre de la première relation.
au membre de la première relation.
![]() est le rapport entre le nombre de cas favorables à
est le rapport entre le nombre de cas favorables à ![]() et le
nombre total de cas possibles.
et le
nombre total de cas possibles.
![]() . Si
. Si ![]() désigne
l'événement ``le
désigne
l'événement ``le ![]() -ème invité a eu son propre
chapeau'', la probabilité
-ème invité a eu son propre
chapeau'', la probabilité ![]() recherchée vaut :
recherchée vaut :