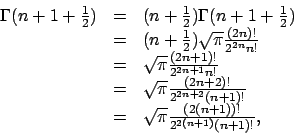suivant: À propos de ce
Intégrales Eulériennes
La fonction gamma a été introduite par Euler afin de généraliser la
fonction factorielle pour des valeurs non entières. Elle a été étudiée
plus tard par des mathématiciens éminents, tels que Legendre, Gauss,
Liouville, Wierestarss, Hermite et beaucoup d'autres en raison de son
importance en analyse mathématique.
Définition. Soit 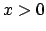 un réel donné. Posons :
un réel donné. Posons :
Nous avons alors :
Théorème 1. Pour tout 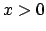 :
:
ou encore :
Démonstration. Il suffit d'appliquer le changement de variable
 pour prouver la première formule et le changement de
variable
pour prouver la première formule et le changement de
variable 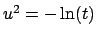 pour la seconde.
pour la seconde.
Ce théorème montre que la fonction gamma 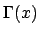 (appelée
aussi intégrale eulérienne) est bien définie pour
(appelée
aussi intégrale eulérienne) est bien définie pour 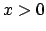 .
.
Valeurs Particulières de 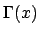
Rappelons d'abord un résultat bien connu sur l'application de changement en
coordonnées polaires :
Théorème 2. Soit  une partie fermée et bornée de
une partie fermée et bornée de
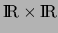 . Soit
. Soit  une application continue sur
une application continue sur  . Désignons
par ailleurs, par
. Désignons
par ailleurs, par 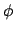 l'application qui associe les coordonnées
cartésiennes d'un point à ses coordonnées polaires :
l'application qui associe les coordonnées
cartésiennes d'un point à ses coordonnées polaires :
Alors :
Application . Soit
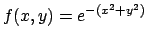 . Nous avons en vertu
du théorème précédent :
. Nous avons en vertu
du théorème précédent :
Par ailleurs :
d'où :
Théorème 3. Nous avons :
et
Démonstration. La première équation est évidente et la seconde
se démontre en utilisant l'intégration par partie.
On en déduit :
Théorème 4. Pour tout
 :
:
Il existe aussi des expressions closes pour 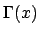 , lorsque
, lorsque 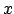 est de
la forme
est de
la forme 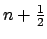 , où
, où
 :
:
Théorème 5. Nous avons :
et
Démonstration. Pour le calcul de
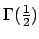 , nous
effectuons le changement de variable
, nous
effectuons le changement de variable 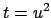 . Il vient :
. Il vient :
Mais cette dernière intégrale vaut
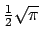 (voir l'application ci-dessus). Nous avons donc
(voir l'application ci-dessus). Nous avons donc
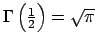 .
.
Pour montrer la seconde égalité, procédons par une récurrence sur
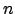 . Pour
. Pour 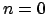 , elle devient l'égalité précédente. Supposons-la vraie
pour
, elle devient l'égalité précédente. Supposons-la vraie
pour 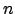 et montrons-la pour
et montrons-la pour  . On a en vertu du théorème
4 :
. On a en vertu du théorème
4 :
ce qui établit le théorème.



suivant: À propos de ce
Maylis Delest
2004-11-03
![]() :
:
![]() pour prouver la première formule et le changement de
variable
pour prouver la première formule et le changement de
variable ![]() pour la seconde.
pour la seconde.
![]() (appelée
aussi intégrale eulérienne) est bien définie pour
(appelée
aussi intégrale eulérienne) est bien définie pour ![]() .
.
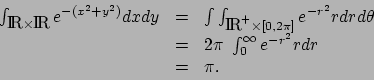
![]() :
:
![]() , lorsque
, lorsque ![]() est de
la forme
est de
la forme ![]() , où
, où
![]() :
:
![]() (voir l'application ci-dessus). Nous avons donc
(voir l'application ci-dessus). Nous avons donc
![]() .
.
![]() . Pour
. Pour ![]() , elle devient l'égalité précédente. Supposons-la vraie
pour
, elle devient l'égalité précédente. Supposons-la vraie
pour ![]() et montrons-la pour
et montrons-la pour ![]() . On a en vertu du théorème
4 :
. On a en vertu du théorème
4 :