table des matières

Université Bordeaux 1

Licence Semestre 5   Méthodes Statistiques pour l'Informatique

Dernière mise à jour effectuée le 22 Janvier 2007

Dénombrements

    Dans tout ce qui suit E est un ensemble fini de cardinal n.

  1. Permutations

    2. Définition Une permutation des éléments de E est un n-uplet (a1,a2,...,an) d'élements de E deux à deux distincts.
    Propriété Le nombre de permutations d'un ensemble à n éléments est n!.

  2. Arrangements

    3. Définition Un arrangement de p objets e E est un p-uplet (a1,a2,...,ap) d'élements de E deux à deux distincts.
    Propriété Le nombre d'arrangements de p éléments d'un ensemble à n éléments est
    .

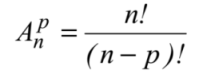  3. Binomial

    4. La notion d'ordre disparait.
    Définition On appelle combinaison de p objets de l'ensemble E tout sous ensemble de E de cardinal p.
    Propriété Le nombre de combinaison de p éléments d'un ensemble à n éléments est
    .

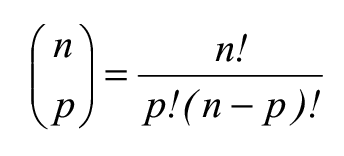  4. Puissance

    5. La notion de répétition apparait.
    Propriété Le cardinal du produit cartésien Ek est nk.