Dans cette section nous allons regarder un algorithme performant conçu par G. Dantzig en 1947. Il est performant d'une part parce qu'il effectue assez peu d'itérations de son opération de base (avancer d'une solution réalisable de base à une autre meilleure) et d'autre part parce que chacune de ces opérations est effectuée par des calculs algébriques simples.
A chaque itération l'algorithme a une solution réalisable de base (nous allons voir comment la première est trouvée) et essaie de trouver une autre solution réalisable de base qui est adjacente en tant que sommet du polytope de solutions réalisables et meilleure (possède une meilleure valeure de la fonction économique). S'il n'existe pas de telle solution meilleure adjacente, la solution actuelle est forcément optimale.
Bien que théoriquement ce processus puisse parcourir un nombre exponentiel de sommets du polytope, en pratique on trouve que le nombre réellement parcourus est petit, ce qui permet à l'algorithme de résoudre facilement des programmes avec des centaines de variables.
Une solution de base étant donnée par l'intersection de ![]() des (hyper)plans
définis par les contraintes, une arête du polytope passant par cette solution
est donnée par l'intersection de
des (hyper)plans
définis par les contraintes, une arête du polytope passant par cette solution
est donnée par l'intersection de ![]() parmi ces hyperplans et, donc,
une solution adjacente est donnée par l'intersection de
parmi ces hyperplans et, donc,
une solution adjacente est donnée par l'intersection de ![]() des
hyperplans plus un nouveau. Si on choisit l'hyperplan à supprimer
de telle façon que l'arête va dans une bonne direction (valeur de la
fonction économique augmentante), une bonne solution adjacente
est donnée par la prochaine intersection entre cette arête et un autre
hyperplan donné par une nouvelle contrainte.
des
hyperplans plus un nouveau. Si on choisit l'hyperplan à supprimer
de telle façon que l'arête va dans une bonne direction (valeur de la
fonction économique augmentante), une bonne solution adjacente
est donnée par la prochaine intersection entre cette arête et un autre
hyperplan donné par une nouvelle contrainte.
Calcul efficace d'une solution réalisable adjacente
Le calcul d'une bonne solution adjacente s'avère très simple dans le
cas où la solution actuelle a ![]() pour tout
pour tout ![]() .
Notons d'abord que dans ce cas
.
Notons d'abord que dans ce cas
![]() étant une solution
réalisable, chaque contrainte
étant une solution
réalisable, chaque contrainte
![]() a forcément
a forcément ![]() .
.
Les arêtes du polytope passant par cette solution sont les ![]() droites
sur lesquelles
droites
sur lesquelles ![]() des variables restent nulles. Prenons par exemple
celle sur laquelle toutes les variables sauf
des variables restent nulles. Prenons par exemple
celle sur laquelle toutes les variables sauf ![]() sont nulles; si la
fonction économique est
sont nulles; si la
fonction économique est
![]() , sa valeur sur cette ligne
est donnée par
, sa valeur sur cette ligne
est donnée par ![]() et, donc, devient positive si
et, donc, devient positive si ![]() .
C'est-à-dire qu'il faut choisir un
.
C'est-à-dire qu'il faut choisir un ![]() positif; parmi les
positif; parmi les ![]() positifs,
on peut choisir arbitrairement. Toujours sur cette ligne, une contrainte comme
positifs,
on peut choisir arbitrairement. Toujours sur cette ligne, une contrainte comme
![]() devient simplement
devient simplement
![]() et, si
et, si
![]() ,
, ![]() n'est pas contrainte; si
n'est pas contrainte; si ![]() , on sait
que
, on sait
que ![]() ne peut pas dépasser
ne peut pas dépasser
![]() sans sortir du polytope.
Enfin le minimum parmi ces rapports
sans sortir du polytope.
Enfin le minimum parmi ces rapports
![]() pour les
pour les ![]() positifs doit donner la valeur de
positifs doit donner la valeur de ![]() à la solution adjacente.
à la solution adjacente.
Ainsi, si la solution actuelle est
![]() , trouver une bonne
solution adjacente est facile et rapide. L'astuce de l'algorithme du simplexe
est d'ajouter de nouvelles variables de telle façon que toute solution
de base est
, trouver une bonne
solution adjacente est facile et rapide. L'astuce de l'algorithme du simplexe
est d'ajouter de nouvelles variables de telle façon que toute solution
de base est
![]() par rapport à un sous-ensemble bien
choisi de
par rapport à un sous-ensemble bien
choisi de ![]() variables.
variables.
Concrètement, pour chaque contrainte
![]() on ajoute une variable d'écart
on ajoute une variable d'écart ![]() définie par
définie par
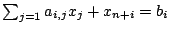 ;
; ![]() sera forcément
nulle à une solution de base située sur l'hyperplan
sera forcément
nulle à une solution de base située sur l'hyperplan
 et sera positive à chaque autre solution
réalisable.
et sera positive à chaque autre solution
réalisable.
Maintenant on a ![]() variables et
variables et ![]() équations (contraintes d'égalité)
et les seules autres contraintes sont que toutes les variables sont
équations (contraintes d'égalité)
et les seules autres contraintes sont que toutes les variables sont ![]() ;
à une solution réalisable de base, on a toujours
;
à une solution réalisable de base, on a toujours ![]() des variables nulles
et les autres (les variables de base), en général, sont positives.
A chaque itération on va choisir une nouvelle base afin de garder les deux
conditions qui rendaient facile le calcul d'une solution adjacente:
des variables nulles
et les autres (les variables de base), en général, sont positives.
A chaque itération on va choisir une nouvelle base afin de garder les deux
conditions qui rendaient facile le calcul d'une solution adjacente:
la fonction économique est donnée par une expression linéaire dans les variables hors base,
chaque variable de base est donnée par une une expression linéaire dans les variables hors base.
Un calcul assez simple calcule ces expressions linéaires pour la nouvelle base permettant de commencer la prochaine itération.
On a une matrice ![]() de
de ![]() lignes et
lignes et ![]() colonnes un vecteur colonne
colonnes un vecteur colonne ![]() et un vecteur ligne
et un vecteur ligne ![]() ; les contraintes d'égalité sont
; les contraintes d'égalité sont ![]() et la fonction économique est
et la fonction économique est
![]() ; les colonnes de
; les colonnes de ![]() correspondant aux variables de la base constituent une matrice de permutation,
c'est-à-dire une matrice carrée (
correspondant aux variables de la base constituent une matrice de permutation,
c'est-à-dire une matrice carrée (![]() par
par ![]() ) où tous les éléments sont
nuls sauf un élément égal à
) où tous les éléments sont
nuls sauf un élément égal à ![]() en chaque ligne et chaque colonne; les
éléments de
en chaque ligne et chaque colonne; les
éléments de ![]() correspondant à ces mêmes variables sont tous nuls.
correspondant à ces mêmes variables sont tous nuls.
On choisit un élément positif ![]() de
de ![]() ; la variable
; la variable ![]() va entrer
dans la base; s'il n'y en a pas, la solution actuelle est optimale;
va entrer
dans la base; s'il n'y en a pas, la solution actuelle est optimale;
parmi les ![]() qui sont positifs, on choisit celui pour lequel le
rapport
qui sont positifs, on choisit celui pour lequel le
rapport
![]() est maximal; la ligne
est maximal; la ligne ![]() a un seul élément
a un seul élément
![]() pour
pour ![]() une variable de la base; c'est cette variable
une variable de la base; c'est cette variable ![]() qui va sortir de la base;
qui va sortir de la base;
![]() est le pivot et on va procéder à une opération de pivotage:
est le pivot et on va procéder à une opération de pivotage:
on divise la ligne ![]() et
et ![]() par
par ![]() ;
;
pour chaque ![]() différent de
différent de ![]() on ajoute à la ligne
on ajoute à la ligne ![]() et à
et à
![]() le multiple de la ligne
le multiple de la ligne ![]() et
et ![]() par
par
![]() , ainsi réduisant
, ainsi réduisant
![]() à zéro;
de la même façon on ajoute à
à zéro;
de la même façon on ajoute à ![]() le multiple
le multiple
![]() de la ligne
de la ligne ![]() ,
réduisant
,
réduisant ![]() à zéro.
à zéro.
Et on a réproduit les conditions énoncées pour la nouvelle base.
On peut noter que si, quand on cherche les ![]() positifs, il n'y en a pas,
on a trouvé un cas ou la fonction objective n'admette aucune borne
supérieure finie.
positifs, il n'y en a pas,
on a trouvé un cas ou la fonction objective n'admette aucune borne
supérieure finie.
Trouver une solution réalisable initiale
Si
![]() n'ést pas une solution réalisable,
une astuce permet de trouver une solution de base réalisable (s'il y'en a)
avec une première application du simplexe à un programme auxiliaire
et ensuite de continuer directement à la solution souhaitée avec une deuxième
application (méthode en deux phases.)
n'ést pas une solution réalisable,
une astuce permet de trouver une solution de base réalisable (s'il y'en a)
avec une première application du simplexe à un programme auxiliaire
et ensuite de continuer directement à la solution souhaitée avec une deuxième
application (méthode en deux phases.)
![]() n'ést pas une solution réalisable parce que quelques uns des
n'ést pas une solution réalisable parce que quelques uns des
![]() sont strictement négatifs; on ajoute une nouvelle variable artificielle
(disons
sont strictement négatifs; on ajoute une nouvelle variable artificielle
(disons ![]() )
avec sa contrainte implicite
)
avec sa contrainte implicite ![]() ,
et pour chaque
,
et pour chaque ![]() avec
avec ![]() on modifie la contrainte numéro
on modifie la contrainte numéro ![]() en ajoutant
en ajoutant ![]() à gauche, les autres contraintes restant inchangées;
maintenant les contraintes sont faisables avec
(par exemple)
à gauche, les autres contraintes restant inchangées;
maintenant les contraintes sont faisables avec
(par exemple)
![]() et toutes les autres variables nulles.
et toutes les autres variables nulles.
Avec ces contraintes et la solution initiale réalisable de base
![]() on maximise la fonction
on maximise la fonction ![]() ;
ceci est le programme auxiliaire.
Si on trouve une solution optimale avec
;
ceci est le programme auxiliaire.
Si on trouve une solution optimale avec ![]() , on a trouvé une solution
réalisable du programme initial; sinon il n'existe pas de telle solution.
, on a trouvé une solution
réalisable du programme initial; sinon il n'existe pas de telle solution.
Qui plus est, quand on a trouvé une solution avec ![]() , en supprimant
la variable artificielle
, en supprimant
la variable artificielle ![]() et en modifiant la fonction objective de départ
(avec les mêmes pivotages utilisés dans la première phase),
on a directement une solution réalisable de base du programme initial
et le tableau qu'il faut pour y appliquer la méthode du simplexe.
et en modifiant la fonction objective de départ
(avec les mêmes pivotages utilisés dans la première phase),
on a directement une solution réalisable de base du programme initial
et le tableau qu'il faut pour y appliquer la méthode du simplexe.
(On va voir un exemple au lieu de démonstration.)
Un problème : les solutions dégénérées
Un petit problème embêtant est celui des solutions dégénérées: quand une solution
de base est l'intersection d'un nombre strictement supérieur à ![]() de contraintes,
il est possible que l'opération de pivotage remplace une de ces contraintes
par une autre, produisant une amélioration nulle dans la fonction objective,
et même que celui-ci se réproduit dans une boucle de façon que l'algorithme
ne termine pas. Parmi plusieurs solutions possibles à ce problème est la
règle de Bland: parmi les candidats pour la colonne ou la ligne du pivot,
quand il y'en a plusieurs, choisir toujours celui de l'indice minimum.
Cette règle est opposée à l'intuition qui dit qu'il faudrait choisir
le coefficient maximum dans la fonction objective mais le risque de non terminaison
est sérieux; en effet des programmes réels sont souvant de type dégénéré.
de contraintes,
il est possible que l'opération de pivotage remplace une de ces contraintes
par une autre, produisant une amélioration nulle dans la fonction objective,
et même que celui-ci se réproduit dans une boucle de façon que l'algorithme
ne termine pas. Parmi plusieurs solutions possibles à ce problème est la
règle de Bland: parmi les candidats pour la colonne ou la ligne du pivot,
quand il y'en a plusieurs, choisir toujours celui de l'indice minimum.
Cette règle est opposée à l'intuition qui dit qu'il faudrait choisir
le coefficient maximum dans la fonction objective mais le risque de non terminaison
est sérieux; en effet des programmes réels sont souvant de type dégénéré.