Pourquoi les contraintes d’intégrité ?
La méthode du simple permet de trouver la solution optimale d’une fonction linéaire économique face à des contraintes du type linéaire. Elle autorise des variables de signes quelconques et peut aussi les astreindre à être positives (ou négatives). Dans beaucoup de circonstances réelles, les variables ne peuvent être que de type entiers. Il arrive en effet fréquemment que le choix imposé doit respecter la règle d’intégrité. Malheureusement ce type de contraintes ne peut pas être traité directement par l’algorithme de simplexe.
Exemple illustratif. :
Un produit es disponible dans des paquets de 20kg de prix de
50€ ou des paquets de 40kg de prix de 80€. Un client, qui a d’au moins de
100kg
du produit cherche à en acheter au moindre coût possible. La contrainte d’intégrité qui
s’oppose tout naturellement ici, implique qu’il ne peut pas en acheter la moitié ou deux
tiers de paquet. Soient
![]() et
et ![]() les nombres respectifsde paquets que le client va acheter. Le programme linéaire suivant formalise le
problème :
les nombres respectifsde paquets que le client va acheter. Le programme linéaire suivant formalise le
problème :
|
minimiser
|
Effet des contraintes d’intégrité
Dans le problème illustratif, si l’on enlève la contrainte
d’intégrité de
![]() le problème devient très simple. En effet puisque le prix du
produit dans le paquet de 20kg est de 2,5 €/kg et dans le paquet de 50kg est de
2€/kg, le client pourrait acheter 2,5 paquets de contenance de 80kg et cela lui
coûterait
le problème devient très simple. En effet puisque le prix du
produit dans le paquet de 20kg est de 2,5 €/kg et dans le paquet de 50kg est de
2€/kg, le client pourrait acheter 2,5 paquets de contenance de 80kg et cela lui
coûterait ![]() . Malheureusement, la contrainte d’intégrité lui impose de
remplacer le nombre 2,5 par 3, et cela lui coûterait
. Malheureusement, la contrainte d’intégrité lui impose de
remplacer le nombre 2,5 par 3, et cela lui coûterait ![]() Or, il existe une solution moins coûteuse : 2 paquets de 40kg et un paquet de 20kg, coûtant
au total de 130€.
Or, il existe une solution moins coûteuse : 2 paquets de 40kg et un paquet de 20kg, coûtant
au total de 130€.
Cet exemple simple montre que l’arrondissement de la solution optimale d’un programme linéaire et nombres réels n’aboutit pas nécessairement à une solution optimale pour le même problème avec la contrainte d’intégrité.
On peut être tenté de confirmer maintenant que du moment où la recherche d’un solutions optimale pour un programme linéaire en nombre d’entrées se fait dans un ensemble plus restreint, la méthode de résolution doit être plus simple que ce même problème sans la contrainte d’intégrité. C’est une confirmation tout à fait erronée. En effet, alors que l’algorithme du simplexe fournit une solution satisfaisante pour les programmes linéaire en nombres réels, on démontre que le problème de programmation linéaire en nombres entiers s’apparente à une classe de problème, appelés problèmes NP-complets, qui sont considérés comme des problèmes algorithmiquement difficiles. Il s’agit d’un ensemble de problèmes de décision qui ont été démontrés être polynomialement équivalents. On ne connaît pas d’algorithmes de décision en temps polynomial pour ces problèmes, sans avoir prouvé que la difficulté est de nature intrinsèque. Quoiqu’il en soit on admet en général que ces problèmes et, donc, celui de programmation linéaire en nombres entiers est de nature difficile.
Forme standard d’un programme linéaire en nombres entiers.
Tout programme linéaire en nombres entiers s’écrit sous la forme :
|
maximiser
|
Où c est un vecteur de ![]()
![]() une matrice à m lignes et n colonnes et
une matrice à m lignes et n colonnes et
![]() On peut transformer un problème de maximisation ou un problème avec contraintes de type
On peut transformer un problème de maximisation ou un problème avec contraintes de type
![]() (au lieu de
(au lieu de ![]() ) en un problème sous cette forme, en appliquant les méthodes
utilisées en programmation linéaire.
) en un problème sous cette forme, en appliquant les méthodes
utilisées en programmation linéaire.
Les problèmes d’optimisation, où des contraintes d’intégrité interviennent, ont un champ d’application très vaste. On peut en énumérer, à titre d’exemple, production en séries, allocations de ressources, localisation des sites, exploitations des mimerais , investissement, et programme des vols d’avions. D’autres applications de programmes linéaires se trouvent en calculs scientifiques tels que les problèmes d’optimisation combinatoires dans un contexte d’ingénierie ou mathématico-physique.
Une instance très particulière des programmes linéaire qui, malgré sa simplicité apparente, se classifie dans les problèmes difficiles est celui du sac-à-dos (knapsack en anglais).
Ce problème s’énonce ainsi :
Un randonneur peut faire un certain nombre de choix parmi
les n nourritures disponibles numérotées
![]() Chaque nourriture i possède un volume
Chaque nourriture i possède un volume
![]() et sa valeur nutritive
et sa valeur nutritive
![]() . Le sac à dos du randonneur a une capacité
. Le sac à dos du randonneur a une capacité ![]() à ne pas dépasser. Le randonneur souhaite alors à faire un menu qui maximise
la valeur nutritive totale. Désignons par
à ne pas dépasser. Le randonneur souhaite alors à faire un menu qui maximise
la valeur nutritive totale. Désignons par ![]() la quantité de la nourriture i que le randonneur va prendre
(si
la quantité de la nourriture i que le randonneur va prendre
(si ![]() la nourriture i n’est
pas choisie, si
la nourriture i n’est
pas choisie, si ![]() elle est choisie). Le
problème du sac-à-dos s’écrit alors :
elle est choisie). Le
problème du sac-à-dos s’écrit alors :
|
maximiser |
|
Il existe une variante de ce problème légèrement plus
générale : on suppose que toute nourriture j est disponible en quantité
![]() (
(
![]() entier).
Les contraintes
entier).
Les contraintes ![]() dans cette invariante deviennent alors :
dans cette invariante deviennent alors :
![]()
La version initiale est appelée par certains auteurs ‘‘programme linéaire en variables bivalentes’’. Ces deux variantes de problème du sac-à-dos et d’autres variables sont liées à un bon nombre de problèmes d’optimisation combinatoire. Etant tous liés au problèmes difficiles. A bondonnant une recherche entièrement algébrique, les informaticiens se limitent à des méthodes de résolutions ‘‘approximatives’’, appelées heuristiques pour aborder ces problèmes dans toute leur généralité. Ces recours ne sont pas tout à fait satisfaisants, dans la mesure où l’heuristique ne fournit pas toujours la solution exacte et elle n’est pas non plus à l’abri d’une complexité exponentielle.
Il existe de nombreuses méthodes, qui avec de divers degré de succès, s’appliquent aux programmes linéaires en variables aléatoires. Les techniques les plus populaires sont fondées sur séparation et évaluation (branch and bound en anglais).
Méthode par séparation et évaluation
Soit à résoudre le programme :
|
maximiser
|
|
Soit z la valeur maximum de la fonction objective ![]() .
.
Etape 1. On considère le programme linéaire relaxé (i.e. sans contrainte d’intégrité).
La méthode simplexe s’applique et l’on peut trouver une solution
optimale (![]() ).
).
![]() est évidemment un majorant de
est évidemment un majorant de ![]() dans une initial. Il n’est pas nécessairement réalisable, puisque la solution trouvée peut ne pas respecter les contraintes
d’intégrité.
dans une initial. Il n’est pas nécessairement réalisable, puisque la solution trouvée peut ne pas respecter les contraintes
d’intégrité.
Etape 2. Si ![]() on considère deux
programmes linéaires relaxés, l’un avec la contrainte supplémentaire
on considère deux
programmes linéaires relaxés, l’un avec la contrainte supplémentaire ![]() et l’autre avec
et l’autre avec ![]() (appelée branche
gauche et branche droite respectivement). La résolution éventuelle de chacune
des branches (s’elle admet une solution) permet de trouver deux solutions plus
restrictives (mais pas nécessairement réalisables).
(appelée branche
gauche et branche droite respectivement). La résolution éventuelle de chacune
des branches (s’elle admet une solution) permet de trouver deux solutions plus
restrictives (mais pas nécessairement réalisables).
Etape 3. On continue l’étape 2 pour une des variables qui n’a pas reçu une valeur entière et cela pour chacune des branches.
Il est évident qu’à chaque branchement les valeurs trouvées pour z seront plus petites et donc, en descendant une branche de l’arborescence, on finira soit par l’irréalisablité du programme linéaire relaxé avec des contraintes associées au branchement soit par une solution entière optimale.
Une comparaison finale des branches abouties permet de trouver la solution optimale entière recherchée.
Exemple 1. Soit :
|
maximiser
|
|
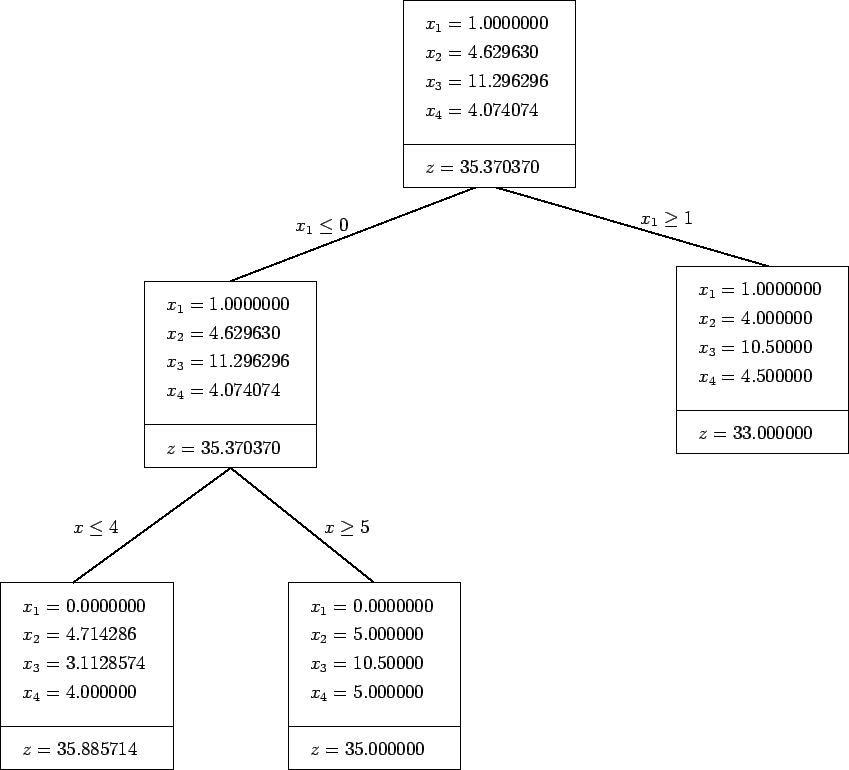
|
| Solution optimale |
Exemple 2. (Une application de la programmation dynamique)
L’exemple suivant est emprunté à D. Sills. Soit le problème du sac-à-dos :
|
maximiser
|
|
On suppose ![]() et
et ![]() sont positifs et
sont positifs et
![]() Nous utilisons la
méthode de programmation dynamique pour aborder ce problème.
Nous utilisons la
méthode de programmation dynamique pour aborder ce problème.
Cherchons dans un premier temps la solution optimale du
problème relaxé. Soit ![]() cette solution et soit
cette solution et soit
![]() la valeur de la
fonction objective pour cette solution. Désignons par
la valeur de la
fonction objective pour cette solution. Désignons par ![]() le vecteur formé des
valeurs entières par défaut de
le vecteur formé des
valeurs entières par défaut de ![]()
![]() est alors une solution
réalisable du problème. Donc la valeur optimale recherchée se trouve dans
l’intervalle
est alors une solution
réalisable du problème. Donc la valeur optimale recherchée se trouve dans
l’intervalle 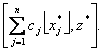
Soit maintenant ![]()
![]() est donc la valeur maximum de la fonction objective,
lorsqu’on remplace
est donc la valeur maximum de la fonction objective,
lorsqu’on remplace ![]() et
et ![]() Calculons
Calculons ![]() pour
pour
![]() tenant compte de
tenant compte de
![]() et
et
![]()
On peut poser ![]() La formule pour
La formule pour ![]() correspond au fait que le problème du sac-à-dos pour un
volume
correspond au fait que le problème du sac-à-dos pour un
volume ![]() à ne pas dépasser
consiste à remplir le sac d’abord d’un volume
à ne pas dépasser
consiste à remplir le sac d’abord d’un volume ![]() et ajouter ensuite un article de volume
et ajouter ensuite un article de volume
![]() ; on choisit donc l’indice j qui maximise
; on choisit donc l’indice j qui maximise ![]() La deuxième solution
pour
La deuxième solution
pour ![]() est la solution
optimale.
est la solution
optimale.
Exemple numérique.
Soit
|
maximiser
|
|
Solution : Dans le problème relaxé le rapport
‘‘quantité-prix’’, montre que le randonneur a l’intérêt de prendre la 1ère
nourriture au maximum et cela fournit la solution ![]() , donnant la valeur
, donnant la valeur
![]() à la fonction
objective. La solution arrondie vaut alors
à la fonction
objective. La solution arrondie vaut alors
![]() donnant la valeur 44 à la fonction objective. Donc la valeur
optimale de
donnant la valeur 44 à la fonction objective. Donc la valeur
optimale de ![]() doit satisfaire
doit satisfaire ![]()
Appliquons maintenant l’algorithme de programmation dynamique à cette instance du problème du sac-à-dos.
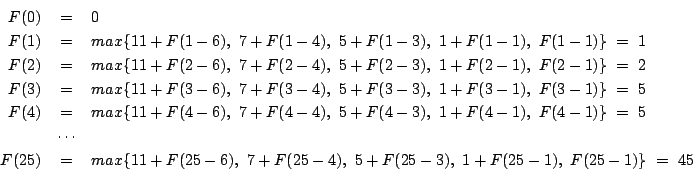
On en déduit alors que la valeur nutritive maximale que la
randonneur peut placer dans son sac-à-dos est de 45, obtenu en choisissant le
menu ![]()
Questionnaire de compréhension immédiate