
Dans la construction simulatrice de la liste d'événements, là où des aléas interviennent, nous avons besoin de tirer une v.a. suivant une distribution donnée. Il est donc nécessaire d'alimenter le programme de constructions d'une suite de tels nombres ou faute de possibilité d'une suite possédant les propriétés similaires.
Initialement des statisticiens utilisaient des tables de taille énorme pour stocker une suite de nombres supposés être aléatoires. Aujourd'hui il existe des techniques bien plus performantes qui permettent de générer rapidement des dizaines de millions de nombres sans encombrement de mémoire. Mais qu'est-ce qu'une suite aléatoire d'entiers ? La réponse à cette question n'est pas simple et déborde du cadre modeste de notre étude. Intuitivement, si nous acceptons que l'aléatoire nécessite l'imprédictibilité, le prochain élément ne peut pas être déterminé du passé. Or cette exigence semble en contradiction avec le concept actuel d'ordinateurs et d'algorithmes qui fonctionnent de façon tout à fait déterministe. Face à cette barrière conceptuelle, on se borne à des suites de nombres dites pseudo-aléatoires. Il s'agit alors d'une suite de nombres qui est statistiquement « indiscernable » d'une suite de nombres aléatoires. Cette terminologie, fondée sur une comparaison avec une suite de nombres vraiment aléatoires, ne présente d'intérêt pratique que si nous fournissons une définition de l'indiscernabilité avec une suite de nombres aléatoires.
Or, si des tests statistiques permettent d'infirmer la vraisemblance d'une hypothèse (ici l'indiscernabilité) ils ne peuvent admettre sa validité face à toute épreuve.
Nous appelons suite uniforme de nombres pseudo-aléatoires (ou suite de nombres aléatoires en bref) une suite d'éléments appartenant à un intervalle fini d'entiers I, satisfaisant les critères ci-dessous :
Absence de périodicité. Le générateur ne doit pas répéter de séquences de nombres lors de générations d'un grand nombre d'éléments.
Indépendance statistique. Les entiers successifs engendrés ne doivent pas être « liés ». Un test statistique permet de confirmer l'absence de corrélation.
Uniformité de distribution. La suite doit être uniformément répartie dans l'intervalle I. Des tests statistiques permettent de mettre à l'épreuve cette propriété pour la suite engendrée.
Pour des raisons techniques, un bon générateur doit également satisfaire les exigences suivantes :
Rapidité. Durant une simulation un grand nombre de v.a. sont à engendrer et, donc, la complexité de cette génération peut peser sur la complexité de l'algorithme.
Reproductibilité. Il est aussi souhaitable que la suite puisse se refaire de façon identique d'une exécution à une autre. Cette exigence est motivée par les soucis de recherche d'erreurs dans le programme de simulation. En effet, ces derniers sont souvent de nature complexe et la détection des erreurs nécessite souvent une répétition du même processus d'exécution.
Il existe de nombreuses méthodes de générations uniformes de nombres pseudo-aléatoires. Nous en exposons une et concluons avec un complément qui permet d'en améliorer considérablement la puissance.
Méthode congruentielle
La méthode est très simple dans son principe. On choisit deux entiers positifs, le premier m appelé multiplicateur et le second p appelé module. Commençons avec un entier positif 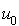 , appelé semence.
, appelé semence.
La suite est définie par la récurrence : 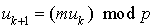 .
.
Lorsque les 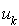 sont différents de 0, les entiers de 1 à
sont différents de 0, les entiers de 1 à  sont engendrés par la formule ci dessus. Alors
sont engendrés par la formule ci dessus. Alors 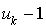 prend valeur de 0 à
prend valeur de 0 à 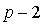 et donc le réel
et donc le réel 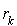 dans
dans 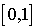 peut être défini par :
peut être défini par : 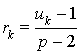 .
.
Si les mots d'ordinateur sont à w bits, nous choisissons 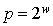 . La multiplication dans la formule récursive produit un résultat à 2 mots ; le mot de puissance inférieure est le résultat de la multiplication mod p. Le calcul de la suite est donc considérablement simplifié.
. La multiplication dans la formule récursive produit un résultat à 2 mots ; le mot de puissance inférieure est le résultat de la multiplication mod p. Le calcul de la suite est donc considérablement simplifié.
Si a n'est pas choisi de façon convenable, on peut avoir 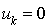 pour
pour 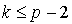 et, donc,
et, donc, 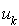 ne prendra pas toutes les valeurs possibles de 1 à
ne prendra pas toutes les valeurs possibles de 1 à  . Pour éviter cet inconvénient, on choisit m tel que
. Pour éviter cet inconvénient, on choisit m tel que  soit un multiple de tous les entiers premiers divisant p.
soit un multiple de tous les entiers premiers divisant p.
Il est également nécessaire que p ne soit pas un multiple de m, sinon pour un certain choix de 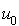 la suite
la suite 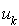 ne couvrira pas l'intervalle entier de 1 à
ne couvrira pas l'intervalle entier de 1 à  .
.
La condition d'absence de corrélation est plus difficile à résoudre et les choix de p et m doivent être suivis d'une analyse statistique des nombres engendrés. Les générateurs souvent utilisés sont fondés sur l'un des choix suivants.
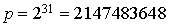 et
et 
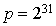 et
et 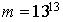
 et
et 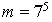 .
.
Une autre variante de la méthode congruentielle est de prévoir une constante additive a, intervenant dans la récurrence qui devient alors : 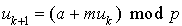 .
.
Méthode de battage
Les méthodes congruentielles ont toutes une périodicité. Dans le cas 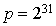 et
et 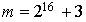 , la période vaut
, la période vaut 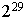 . La technique du battage, pourtant très simple, augmente considérablement la puissance du générateur. On débute avec un tableau de dimension approximative 100 (la dimension exacte n'a pas d'importance). Ce tableau étant rempli de nombres aléatoires obtenus à partir du générateur, le programme de simulation y « pioche » un nombre au hasard quand il en a besoin, l'élément « pioché » est alors remplacé dans le tableau par un autre nombre tiré par le générateur.
. La technique du battage, pourtant très simple, augmente considérablement la puissance du générateur. On débute avec un tableau de dimension approximative 100 (la dimension exacte n'a pas d'importance). Ce tableau étant rempli de nombres aléatoires obtenus à partir du générateur, le programme de simulation y « pioche » un nombre au hasard quand il en a besoin, l'élément « pioché » est alors remplacé dans le tableau par un autre nombre tiré par le générateur.
Il faut noter que cette technique utilise 2 nombres aléatoires pour chaque nombre transmis, le premier indique l'emplacement du nombre pioché dans le tableau, le second sert pour son remplacement.
La méthode générale pour la génération des v.a. de distribution quelconque est la transformation d'une v.a. de distribution uniforme.
Dans la suite, nous considérerons deux types de v.a. non uniformes, les v.a. discrètes prenant des valeurs dans un ensemble dénombrable (fini ou infini) et les v.a. continues.
Cas des variables aléatoires discrètes
Supposons que la v.a. X prenne l'une des valeurs 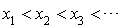 respectivement avec les probabilités
respectivement avec les probabilités 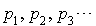 . Si le tirage aléatoire produit la valeur
. Si le tirage aléatoire produit la valeur 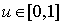 , avec une répartition uniforme.
, avec une répartition uniforme.
Divisons alors l'intervalle 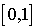 en sous intervalles
en sous intervalles  . Si
. Si 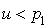 on pose
on pose 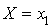 et si
et si 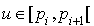 on pose
on pose 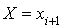 . Il est facile de voir que si u est uniforme alors X prend la valeur
. Il est facile de voir que si u est uniforme alors X prend la valeur 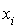 avec la probabilité
avec la probabilité 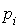 .
.
Cas des variables aléatoires continues
Soit X une v.a. de fonction de répartition 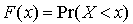 .
.
F est une fonction croissante avec 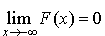 et
et  .
.
Supposons F continue et posons : 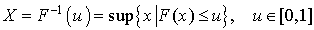 .
.
Nous avons :
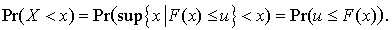
Si U est une v.a. uniforme, cette dernière expression vaut 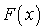 . On en déduit que la v.a.
. On en déduit que la v.a. 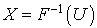 est de fonction de répartition
est de fonction de répartition 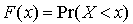 .
.
D'où la méthode suivante pour générer une v.a. X de fonction de répartition F :
Tirer une v.a. uniforme u dans 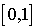 .
.
Poser 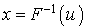 .
.
Exemple
Soit X une v.a. exponentielle de paramètre 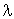 :
: 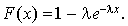
Nous avons 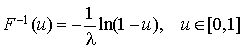 .
.
Donc, pour tirer une v.a. exponentielle de paramètre 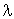 , il faut poser
, il faut poser 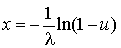 , où u est une v.a. tirée uniformément dans
, où u est une v.a. tirée uniformément dans 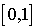 . On simplifiera la méthode en faisant la remarque suivante : si u est uniforme dans
. On simplifiera la méthode en faisant la remarque suivante : si u est uniforme dans 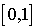 , alors il en est de même pour
, alors il en est de même pour 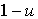 . On peut donc poser
. On peut donc poser  au lieu de
au lieu de 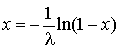 .
.
Certaines applications de la technique de simulation n'ont initialement rien à voir avec des phénomènes aléatoires et encore moins avec des systèmes d'attente. L'introduction de tirages aléatoires permet une approximation de la solution qui peut être inaccessible ou trop complexe par des méthodes déterministes algorithmiques.
Ces instances d'applications de la technique de simulation sont appelées algorithmes de Monte Carlo en raison de leur dépendance de tirages aléatoires. Ces algorithmes sont systématiquement appliqués en physique, mathématiques et informatique en vue d'une approximation de la solution dont la valeur exacte reste hors de portée. Nous ne donnons ici qu'un exemple simple d'application mathématique afin de fournir un aperçu de l'importance de la technique.
Evaluation d'une intégrale (Ecker, Kupferschmid)
Considérons le problème du calcul de l'intégrale suivante :
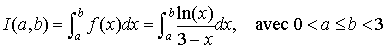 .
.
Cette intégrale n'admet pas de forme close. Pour a et b donnés, on peut calculer la valeur approximative de 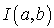 par une méthode déterministe telle que la règle de Simpson. Pour
par une méthode déterministe telle que la règle de Simpson. Pour 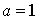 et
et 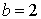 , on obtient
, on obtient 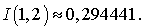 La figure ci-dessous montre le graphe de la fonction à intégrer.
La figure ci-dessous montre le graphe de la fonction à intégrer.
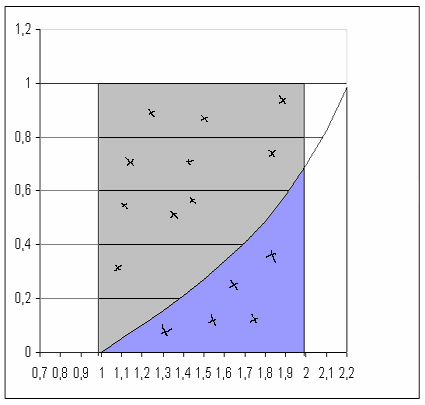
La méthode de Monte Carlo d'intégration consiste à évaluer la portion bleue du rectangle et de la multiplier ensuite par l'aire du rectangle (valant ici 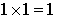 ). Pour estimer cette portion, la méthode propose de tirer des points
). Pour estimer cette portion, la méthode propose de tirer des points 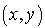 dans le rectangle
dans le rectangle 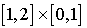 et de déterminer ensuite si le point tiré est au-dessus ou au-dessous de la courbe i.e. si
et de déterminer ensuite si le point tiré est au-dessus ou au-dessous de la courbe i.e. si  ou
ou 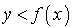 (la probabilité
(la probabilité 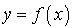 est nulle). La portion recherchée aura alors l'approximation suivante :
est nulle). La portion recherchée aura alors l'approximation suivante :
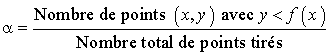
Tout point aléatoire est le résultat de deux tirages x et y, le premier uniformément réparti dans 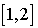 , le second dans
, le second dans 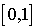 . Pour cela, nous effectuons une suite de tirages uniformes
. Pour cela, nous effectuons une suite de tirages uniformes 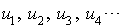 dans
dans 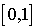 et nous posons :
et nous posons :
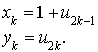
Sur la figure nous avons tiré 15 points (donc 30 tirages pour u) dont 5 sont situés au-dessous de la courbe, nous aurons donc :
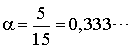
Et la valeur de l'intégrale est alors approximativement :
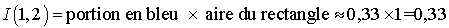 .
.
En vertu de la loi des grands nombres, pour que l'approximation soit plus précise, il est nécessaire de tirer un plus grand nombre de points. Nous aurons la table suivante pour 100, 1000, 10 000, 100 000 et 1 000 000 points :
Nombre de points |
Estimation de |
100 |
0,320000 |
1 000 |
0,278000 |
10 000 |
0,299400 |
100 000 |
0,296040 |
1 000 000 |
0,294538 |
Vraie valeur |
|
On voit que l'approximation converge lentement lorsque le nombre de tirages croît.
Il est à noter que l'exemple cité ne présente qu'une illustration de la méthode et qu'on n'utilise pas cette technique pour évaluer les intégrales simples où les méthodes déterministes d'analyse numérique fournissent des approximations beaucoup plus précises moyennant des algorithmes moins complexes. Néanmoins, dans le cas des espaces de dimensions supérieures, la méthode de Monte Carlo peut s'avérer avantageuse. En effet, l'intégrale calculée peut être le volume d'une région dont les frontières sont caractérisées par des formules complexes rendant le calcul de l'approximation difficile. La méthode de Monte Carlo devient alors pertinente. Cette méthode de simulation pour évaluer des intégrales intervient dans d'importants champs d'application tels que la physique nucléaire et beaucoup de super-ordinateur sont aujourd'hui consacrés entièrement ou partiellement à ces tâches.