Proposition 1 :

Un système  M/M/1 peut se modéliser par un processus de naissance et de mort de taux de naissance constant égal au taux d'arrivée et de taux de mort constant égal au taux de service.

La réponse est oui (voir la définition  M/M/1).
 

Proposition 2 :

Dans un système 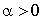 M/M/1, si l'on multiplie le taux de service et le taux de mort par une constante numérique , le nouveau système aura un comportement identique au système initial.

La réponse est oui. Tous les paramètres d'un système 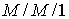sont définis en fonction de 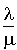et, donc, la multiplication 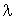de et de 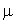par le même nombre 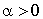les laisse inchangés.

Proposition 3 :

Un système 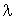 M/M/s de taux d'arrivée et de taux de service 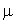par serveur se comporte comme un processus de naissance et de mort de taux de naissance constant 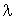et de taux de mort .

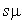La réponse est non. Prenons, en effet, le cas particulier 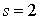. Lorsque le nombre d'usagers dans le système est 1, un seul des serveurs est occupé et donc 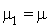ce qui n'est pas égal à .

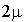Proposition 4 :

Un système 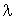 M/M/s de taux d'arrivée et de taux de service 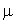par serveur se comporte comme un processus de naissance et de mort avec 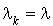et .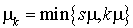

La réponse est oui. Lorsqu'il y a des usagers dans le système le taux de service est .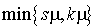
 

Proposition 5 :

Un système M / M / s / K admet un nombre fini d'états.

La réponse est oui. Il n'admet que les états évidents .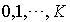
 

Proposition 6 :

Dans un système 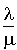 M/M/∞ le nombre moyen d'usagers en attente en régime stationnaire est .

La réponse est oui. En effet le nombre d'usagers dans le système suit une loi de Poisson de paramètre 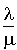(voir le cours).

Proposition 7 :

Le temps passé par usager dans le système est la somme du temps passé en attente et 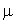(taux de service).

La réponse est oui. C'est évident.