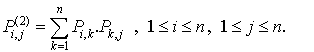
Il s'agit ici de calculer pour une chaîne donnée les probabilités de transition d'un état i à un état j sur une période plus ou moins longue. Si la durée d'attente est finie, nous réalisons des calculs exacts, sinon on peut calculer la tendance, c'est-à-dire que les calculs donnent des probabilités asymptotiques.
Type de calcul
La probabilité d'une transition de l'état i à l'état j en deux étapes est la somme pour tout état intermédiaire k de la probabilité d'une transition de i à k dans la première et d'une transition de k à j dans la deuxième.
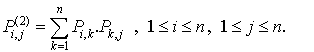
Ces équations se traduisent en équation matricielle :
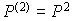 ,
,
où l'élément de la i-ième ligne et la j-ième colonne de la matrice
On peut généraliser le calcul de ces probabilités à m étapes. Pour aller de l'état i à l'état j en m étapes, il est donc facile de définir la matrice des probabilités de transition 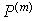 .
.
La probabilité d'une transition de l'état i à l'état j dans m étapes est la somme pour tout état k de la probabilité d'une transition de i à k dans les premières
 .
.
Et, bien sûr, on peut calculer 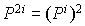 . (Approximativement
. (Approximativement 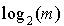 au lieu de
au lieu de
Une variante de ce calcul
Si on effectue ces calculs avec des matrices de valeurs booléennes, où « + » équivaut à « OU » et « 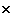 » équivaut à « ET », alors on peut déterminer s'il existe un chemin de longueur m de i à j. Si préalablement on pose
» équivaut à « ET », alors on peut déterminer s'il existe un chemin de longueur m de i à j. Si préalablement on pose 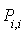 = vrai
= vrai
Avec les matrices booléennes, on évite les erreurs d'arrondis, les calculs sont aussi plus simples et plus rapides (on trouve, donc, un algorithme mais pas forcément le meilleur pour répondre à la question suivante : pour tout couple de sommets
En fait, il existe un autre algorithme classique et très efficace permettant de trouver les plus courts chemins entre chaque couple de sommets (Algorithme de Dijkstra).
Pour savoir si deux états sont dans la même classe, il suffit de décider s'il existe un chemin de longueur inférieur à n de i à j, et un chemin de longueur inférieur à n de j à i, et ainsi on peut trouver toutes les classes de la chaîne de Markov.
Caractéristiques
Pour n'importe quelle configuration initiale d'une chaîne non périodique, les probabilités du système convergent vers une distribution limite. Une fois la distribution limite atteinte, on dit que le système est stationnaire. S'il n'y a qu'une seule classe finale, alors la distribution limite ne dépend pas de la distribution initiale et la distribution limite est l'unique distribution stationnaire. La limite de 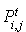 ne dépend pas de i. On peut alors écrire
ne dépend pas de i. On peut alors écrire 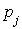 pour cette limite.
pour cette limite.
On peut remarquer que si la configuration initiale est déjà la distribution limite alors elle ne va jamais changer. Donc,
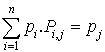
(une équation par colonne de la matrice) où n est le nombre d'états de la chaîne.
Détermination de la distribution limite d'une chaîne
Pour calculer la distribution limite du système, on se rend compte que les n équations linéaires trouvées dans le paragraphe précédent ne suffisent pas. Le vecteur
Il est nécessaire d'ajouter une nouvelle équation indépendante pour réduire le nombre de solutions à 1. Une équation est donnée par le fait évident qu'on a :
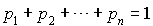
et on trouve, effectivement, que la solution est unique.
Le cas de plusieurs classes finales non périodiques
Avec probabilité 1, le système va terminer dans une classe finale ; pour un état initial donné, on veut savoir la probabilité de chaque classe finale.
La méthode à appliquer est la suivante :
Choisir une classe finale C
Pour chaque état i, définir 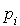 la probabilité pour que la chaîne commençant dans l'état i, à un moment ou à un autre, se trouve dans un état de la classe C. On voit que si i est dans C, alors
la probabilité pour que la chaîne commençant dans l'état i, à un moment ou à un autre, se trouve dans un état de la classe C. On voit que si i est dans C, alors 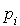 = 1
= 1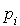 = 0
= 0
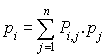
(soit une équation pour chaque ligne de P)
Et cette fois comme les équations sont indépendantes, elles suffisent pour calculer les 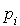 .
.
On peut faire cela pour chaque C finale et la distribution limite pour un état initial i est la somme pondérée des distributions limite de chaque classe finale C avec pour poids la probabilité de tomber en C à partir de l'état i.
Savoir si une classe est périodique ou non
On sait déjà calculer la matrice 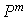 des chemins de longueur
des chemins de longueur
S'il y a deux tels chemins de i à j et k (i, j et k dans la même classe), alors j et k sont dans la même sous-classe
Pour trouver toutes les paires, il suffit de prendre
Le cas périodique
Ici, il n'y a plus de distribution limite, mais pour tout 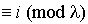 . Voici la méthode a appliquer :
. Voici la méthode a appliquer :
Diviser les états persistants en
Calculer une distribution limite sur chaque sous-classe en utilisant la matrice de transitions en
Pour savoir la probabilité, à l'instant t (t grand) d'être dans un état donné, il faut d'abord calculer la probabilité d'être tombé dans chaque sous-classe. Cette probabilité dépend de
Les probabilités pour
Les autres se déduisent facilement (la probabilité d'être dans la sous-classe 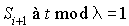 est égale à celle d'être dans la sous-classe
est égale à celle d'être dans la sous-classe 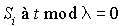 et ainsi de suite).
et ainsi de suite).