Module C1.7 : Processus stochastique et simulation
Les chaînes de Markov
La classification des états
Auteur(s) : Mike Robson - IUP Miage Bordeaux
On classe les états d'une chaîne de Markov en fonction des différentes propriétés qui les caractérisent.
Les états persistants
Un état i est dit persistant ou récurrent si la probabilité de repasser une deuxième fois en i après un premier passage est égale à 1. Il est à noter que cette propriété n'est pas équivalente à un évènement certain (considérer une chaîne à deux états avec les 4 probabilités de transition toutes égales à 0.5 ; même si la probabilité de ne jamais arriver en 2 si on commence en 1 est 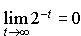 , cet évènement n'est pas impossible). Pour les chaînes finies, cela équivaut à dire que, s'il est possible d'aller de l'état i à un autre état j (éventuellement en plusieurs étapes), il est possible de revenir de j à i. Dans le cas contraire, l'état est dit transitoire.
, cet évènement n'est pas impossible). Pour les chaînes finies, cela équivaut à dire que, s'il est possible d'aller de l'état i à un autre état j (éventuellement en plusieurs étapes), il est possible de revenir de j à i. Dans le cas contraire, l'état est dit transitoire.
Dans chacune des classes définies dans la section précédente, soit tous les états sont persistants soit tous sont transitoires. S'ils sont persistants la classe s'appelle une classe finale; dans le cas contraire elle est dite de passage.
Dans notre exemple les 3 classes {1,2,3}, {4,5,6,7} et {8} sont de passage et les deux autres sont finales. Les classes finales sont celles de degré sortant nul dans le graphe réduit.

Les états ergodiques
Un état i est dit ergodique si le temps moyen entre le premier passage à l'état i et le second est fini.
Remarque : pour les chaînes finies, il n'existe pas de différence entre état persistant et état ergodique.

Les états périodiques
L'état i est dit périodique de période λ > 1, si λ est le plus grand commun diviseur des longueurs des circuits qui passent par i. Autrement dit, la probabilité de passage de i à i en n transitions est nulle sauf si n est un multiple de λ et λ est le plus grand entier ayant cette propriété.
Dans une classe, soit tous les états sont périodiques avec la même période λ, soit aucun n'est périodique. Dans le premier cas, on dit que la classe est périodique. On peut alors diviser la classe en λ sous-classes 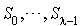 de sorte que chaque transition aille d'un état d'une sous-classe
de sorte que chaque transition aille d'un état d'une sous-classe 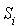 à un état de la sous-classe
à un état de la sous-classe 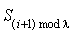 .
.

Exercices
Questionnaire de compréhension immédiate

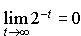 , cet évènement n'est pas impossible). Pour les chaînes finies, cela équivaut à dire que, s'il est possible d'aller de l'état i à un autre état j (éventuellement en plusieurs étapes), il est possible de revenir de j à i. Dans le cas contraire, l'état est dit transitoire.
, cet évènement n'est pas impossible). Pour les chaînes finies, cela équivaut à dire que, s'il est possible d'aller de l'état i à un autre état j (éventuellement en plusieurs étapes), il est possible de revenir de j à i. Dans le cas contraire, l'état est dit transitoire.
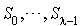 de sorte que chaque transition aille d'un état d'une sous-classe
de sorte que chaque transition aille d'un état d'une sous-classe 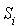 à un état de la sous-classe
à un état de la sous-classe 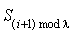 .
.