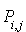 la probabilité d'une transition à l'état j à l'instant
la probabilité d'une transition à l'état j à l'instant
P la matrice de ces probabilités :
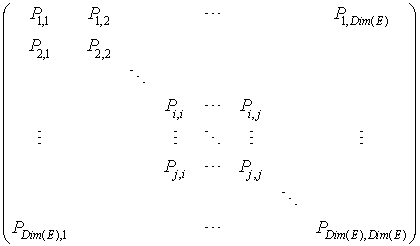
Cette matrice contient les probabilités des transitions envisageables par le système (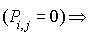 pas de transition possible de i à j).
pas de transition possible de i à j).
Il s'agit de modéliser une chaîne de Markov à l'aide de représentations synthétiques afin de connaître l'évolution des états du système. On utilisera les matrices ou encore les graphes. Soit une chaîne de Markov possédant un ensemble d'états E. On note :
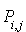 la probabilité d'une transition à l'état j à l'instant
la probabilité d'une transition à l'état j à l'instant
P la matrice de ces probabilités :
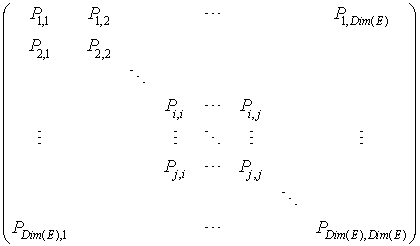
Cette matrice contient les probabilités des transitions envisageables par le système (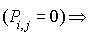 pas de transition possible de i à j).
pas de transition possible de i à j).
Remarque : la matrice n'est pas symétrique, (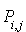 n'est pas forcément égal à
n'est pas forcément égal à  ). En effet, la probabilité de passage de i à j n'est pas en général égale à celle de passage de j à i.
). En effet, la probabilité de passage de i à j n'est pas en général égale à celle de passage de j à i.
Définition Une matrice vérifiant les deux propriétés suivantes : est une matrice stochastisque. |
La matrice d'une chaîne de Markov est forcément stochastique et inversément, toute matrice stochastique est la matrice d'une chaîne de Markov.
Considérons la matrice suivante, il est en effet facile de vérifier que c'est une matrice stochastique, et correspond par conséquent à la matrice d'une chaîne de Markov.

Les éléments de cette matrice sont donnés dans un ordre aléatoire. On verra plus loin qu'il est possible de regrouper les états en des classes de manière à ne plus avoir de grandes dispersions de coefficients non nuls dans la matrice.
Une deuxième représentation : les graphes de transition
Définition générale
Une autre représentation d'une chaîne de Markov permettant de déduire les propriétés qualitatives est le graphe de transition. Ce graphe orienté possède un sommet pour chaque état de la chaîne et un arc d'un sommet vers un autre si la probabilité de cette transition est non nulle.
Il convient de diviser les états d'une chaîne en classes, ensembles tels qu'il existe un chemin en chaque sens entre toute paire de sommets d'une même classe, c'est-à-dire les composantes fortement connexes du graphe de transitions.
Voici notre exemple dans un ordre où ces cinq classes apparaissent, à savoir :


Vocabulaire de la théorie des graphes
Dans un graphe (orienté), on appelle chemin une suite de sommets possibles pour aller d'un sommet à un autre du graphe. Mathématiquement, si  est une suite de sommets telle que, pour tout i tel que
est une suite de sommets telle que, pour tout i tel que 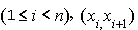 soit un arc, la suite d'arcs
soit un arc, la suite d'arcs  est un chemin de
est un chemin de 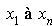 ; il faut noter que le chemin peut être vide (le cas
; il faut noter que le chemin peut être vide (le cas  tel que
tel que
Les sous-ensembles maximaux de sommets, tels qu'entre deux sommets quelconques d'un même sous-ensemble existe un chemin, sont nommés composantes fortement connexes du graphe.
Graphe réduit
Une troisième représentation permettant d'indiquer de façon plus grossière le comportement d'une chaîne, est le graphe réduit où chaque classe est représentée par un sommet et où il y a un arc d'une classe vers une autre, s'il existe une transition d'un état de la première classe vers un état de la deuxième. On obtient alors pour l'exemple ci-dessus le graphe réduit suivant.
