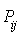 . Dans cette séquence nous définissons le coût moyen d'une transition de i à j par un nouveau coefficient
. Dans cette séquence nous définissons le coût moyen d'une transition de i à j par un nouveau coefficient 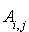 (on suppose que le coût ne dépend ni du temps ni de l'histoire).
(on suppose que le coût ne dépend ni du temps ni de l'histoire).On considère dans cette séquence des chaînes de Markov qui modélisent des phénomènes économiques. Chaque transition du système a un coût associé et on veut se servir du modèle pour analyser et/ou minimiser les coûts moyens à long terme. On ne considèrera que le cas où tous les états sont persistants et apériodiques.
Coût d'une transition
Nous avons vu dans les séquences précédentes que l'on associe à chaque transition d'un état
i à un état j une probabilité 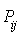 . Dans cette séquence nous définissons le coût moyen d'une transition de i à j par un nouveau coefficient
. Dans cette séquence nous définissons le coût moyen d'une transition de i à j par un nouveau coefficient 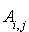 (on suppose que le coût ne dépend ni du temps ni de l'histoire).
(on suppose que le coût ne dépend ni du temps ni de l'histoire).
Coût moyen d'une transition
Le coût moyen de la première transition de l'état i est :
 .
.
Le coût moyen par transition tend vers une constante g. Cette constante est le coût moyen d'une transition dans la distribution limite 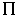 (cf la séquence précédente).
(cf la séquence précédente).
On peut donc facilement calculer g :
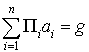
Possibilité de choix
Supposons que dans l'état i on puisse choisir entre plusieurs décisions et que pour la décision d, la probabilité d'aller à l'état
j est 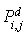 avec un coût
avec un coût 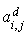 .
.
On peut calculer l'espérance du coût d'une transition :

mais minimiser cette quantité (la politique gloutonne) n'est pas forcément la bonne politique.
De même, le nombre de politiques possibles peut être trop grand et l'on ne peut calculer le coût moyen g de chacune d'elle sans oublier que ce n'est pas forcément la politique possédant le plus petit g qu'il convient de choisir... Comment comparer les coûts que nous devons payer aujourd'hui avec ceux des années futures ?
C'est un compromis entre la politique gloutonne et la minimisation de g. Un euro aujourd'hui est plus utile qu'un euro l'année prochaine; Le coût d'un euro aujourd'hui est plus grand qu'un pareil coût l'année prochaine;
On veut calculer les coûts sur la supposition qu'un euro à l'instant t vaut  euros à l'instant
euros à l'instant 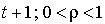 .
.
Rapport avec le taux d'intérêt : si le taux réel d'intérêt (payé ou reçu) est 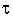 , on a
, on a
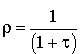
Les équations pour les coûts totaux : On a toujours un coût immédiat (moyen) en l'état i de ai et une probabilité 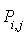 de transition de l'état i à j. Le coût moyen actualisé de toutes les transitions à partir de l'état i, noté vi, est donné par l'équation :
de transition de l'état i à j. Le coût moyen actualisé de toutes les transitions à partir de l'état i, noté vi, est donné par l'équation :
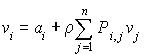
(le coût de la première transition augmenté de l'espérance actualisée des coûts de toutes les transitions après la première)
Ici parce que  nous avons un système non singulier : on peut calculer les
nous avons un système non singulier : on peut calculer les
Calcul d'une politique optimale avec actualisation
On considère maintenant le cas où, dans chaque état, on peut choisir entre plusieurs décisions et on veut minimiser le coût total avec actualisation.
Il est évident que la décision optimale pour chaque état ne dépend ni de l'histoire ni du temps.
On peut utiliser l'algorithme d'amélioration d'une politique initiale : calculer le coût total (avec actualisation) 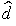 qui minimise
qui minimise 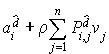 ; répéter tant qu'il y a une réduction ;
; répéter tant qu'il y a une réduction ;
(ce qui équivaut à minimiser le coût qu'on aurait si on choisissait une nouvelle politique pour la première étape et gardait l'ancienne politique après, ce qui explique pourquoi il y a amélioration).
Justification de cet algorithme
Il y a une réduction des coûts à chaque itération.
Le nombre de politiques possibles est fini, donc, il est garanti que l'algorithme se termine.
En principe cette terminaison pourrait être très lente (le nombre de politiques étant très élevé), mais "en pratique" l'algorithme trouve la politique optimale après un nombre raisonnable d'itérations.
Nous donnons une démonstration plus mathématique que l'algorithme réduit les coûts à chaque étape, sauf si on est déjà à une politique optimale :
D'abord avec les décisions d, on a :
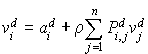
On choisit 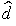 tel que
tel que
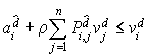
(et on continue si on a une réduction pour au moins un i)
Les vrais nouveaux coûts sont donnés par :
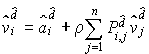
Donc :

(et on a une augmentation pour au moins un i)
Considérons l'indice i qui donne le minimum de 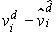 : on a
: on a

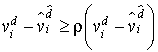
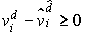
et, donc, 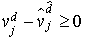 pour tout j
pour tout j
Finalement, le résultat ne peut donc être nul pour tout j, et donc on a une amélioration.
Ce cas est plus compliqué car les équations :
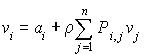
ne sont pas utilisables si  ; (soit aucune solution, soit plusieurs).
; (soit aucune solution, soit plusieurs).
On peut définir 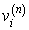 le coût moyen d'une suite de n transitions à partir de l'état i. On trouve que :
le coût moyen d'une suite de n transitions à partir de l'état i. On trouve que :
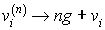
où, maintenant,
On a 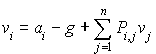 ,
,
mais ces équations ne suffisent pas (ajout de la même constante k à chaque
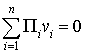
On peut d'optimiser la politique en utilisant la même idée que dans le cas avec actualisation :
Choisir une politique initiale
Calculer 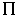 , g et les
, g et les
Utiliser ces
Itérer tant qu'il y a amélioration
Exemple : Assurance d'un véhicule
Le coût de l'assurance d'un véhicule est 100, 200, 400 ou 600.
Après un an sans aucun accident déclaré, le prix est réduit au niveau inférieur.
Après un an avec un accident déclaré, le prix est augmenté au niveau supérieur.
La probabilité d'un accident grave est
La probabilité d'un accident mineur est
Devrait-on déclarer un accident mineur ou payer la réparation ?
(nous prenons 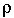 = 0.9
= 0.9
Calcul de la politique optimale
Je commence avec la politique de déclarer tout incident
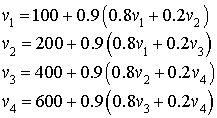
et je calcule 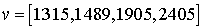
Donc une meilleur politique pour les niveau 200 et 400 est de payer les réparations.
Par exemple pour 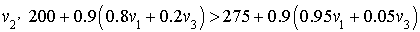 :
:
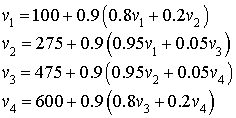
et  .
.
Maintenant on voit qu'une meilleur politique à 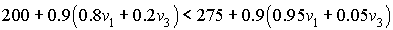 ).
).
Donc, une troisième politique :
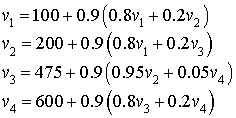
et 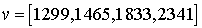 .
.
La solution optimale !
Le modèle n'est pas très réaliste car tous les accidents mineurs n'ont pas le même coût mais ce calcul peut aider à prendre de bonnes décisions, par exemple en l'état 2 déclarer un sinistre si le coût est supérieur à 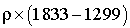 .
.
Questionnaire de compréhension immédiate