Module C1.7 : Processus stochastique et simulation
Qu'est-ce qu'une chaîne de Markov ?
Exercices
Exercice 1 :
Prolongement de l'exercice du cours. Complétez certaines cases du tableau ci-dessous en calculant les probabilités de transition.
Etats d'arrivée |
| |
0 |
1 |
2 |
3 |
4 |
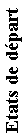 |
0 |
a0 |
a1 |

|

|

|
1 |
a0(b1+b2+b3+b4) |
a0b0+a1(b1+b2+b3+b4) |

|

|

|
2 |

|

|

|

|

|
3 |

|

|

|

|

|
4 |

|

|

|

|

|
Cliquez sur  pour afficher la réponse correspondante (réponse globale).
pour afficher la réponse correspondante (réponse globale).
Exercice 2 :
- On considère un jeu entre 3 joueurs A, B, C avec un total de 4 pieces:
Combien y a-t-il d'états? 
- Dans ce même jeu, les seuls joueurs possédant au moins une pièce
peuvent jouer, si les trois peuvent jouer, on choisit une paire à jouer aléatoirement
avec probabilité uniforme et chacun de ces deux joeurs choisis a
probabilité 1/2 de gagner une pièce de l'autre:
Pour la transition de l'état (A, B, C ont respectivement 2, 1 et 1 pièce)
à l'état (A, B, C ont respectivement 1, 2 et 1 pièce):
- Cette transition nécessite que A joue contre B; quelle est la probabilité
de cet événement?

- Si A joue contre B quelle est la probabilité que A gagne?

- Quelle est la probabilité de la transition?

- Si on regarde le nombre de pièces que possède A, ce nombre change aléatoirement
mais on ne peut pas exprimer ces probabilités de changer par une chaîne de Markov;
pourquoi pas?

Exercice 3 :
- Deux jours ouvrables sur trois, le facteur livre du courrier
à ma boîte à lettres; s'il le fait, je le vois avec
probabilité
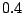 ;
les jours où je l'ai vu, je vide toujours la boîte, mais les autres
jours je cherche le courrier avec probabilité
;
les jours où je l'ai vu, je vide toujours la boîte, mais les autres
jours je cherche le courrier avec probabilité 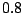 % et je vide la boîte
si j'en trouve.
% et je vide la boîte
si j'en trouve.
Je peux modéliser cette situation par une chaîne de Markov à 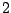 états
(boîte vide ou pleine); quelles sont les probabilités de transition?
états
(boîte vide ou pleine); quelles sont les probabilités de transition?

- A un carrefour au croisement de deux routes la circulation
est contrôlée par des feux tricolores dotés de détecteurs de
l'arrivée de véhicules; dans chaque période de
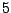 secondes, il y a
probabilité
secondes, il y a
probabilité 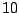 % de l'arrivée d'un véhicule sur la grande route
et
% de l'arrivée d'un véhicule sur la grande route
et 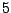 % sur la petite. Quand un véhicule est détecté sur la route pour
laquelle les feux sont rouges, ils seront changés à vert au prochain
multiple de 5 secondes possible en respectant une intervalle de 15 secondes
au moins entre changements.
% sur la petite. Quand un véhicule est détecté sur la route pour
laquelle les feux sont rouges, ils seront changés à vert au prochain
multiple de 5 secondes possible en respectant une intervalle de 15 secondes
au moins entre changements.
- Combien d'états faudra-t-il pour modéliser cette
situation?

- Quelles sont les probabilités de transition?

 |
|
|
 pour afficher la réponse correspondante (réponse globale).
pour afficher la réponse correspondante (réponse globale).


